はじめに
多角形がいくつかの三角形に分割できることからも分かる通り,三角形は図形の基本です。
これまで三角形の辺・角・面積について取り扱いを学んできました。
これで三角形に関する情報は一通り扱った気もしますが,まだ外接円・内接円も残っています。
目次
外接円の半径
外接円の半径については,すでに求め方を学んでいます。
正弦定理を使うんでしたね。
どんな式だったか確認しておきましょう。
\(
\begin{align}
\displaystyle\frac{a}{\sin A} = \displaystyle\frac{b}{\sin B} = \displaystyle\frac{c}{\sin C} = 2R
\end{align}
\)
ある辺と対角の情報がセットで分かれば,外接円の半径を求められるわけですね。
外接円の中心のことを「外心」ということも覚えておきましょう。
内接円の半径
内接円とは,三角形の内部で三角形の3辺すべてに接する円です。
内接円の中心のことを「内心」といいます。
\(\triangle\mathrm{ABC}\)の内心を\(\mathrm{I}\)とすると,内接円は下図の赤い円です。
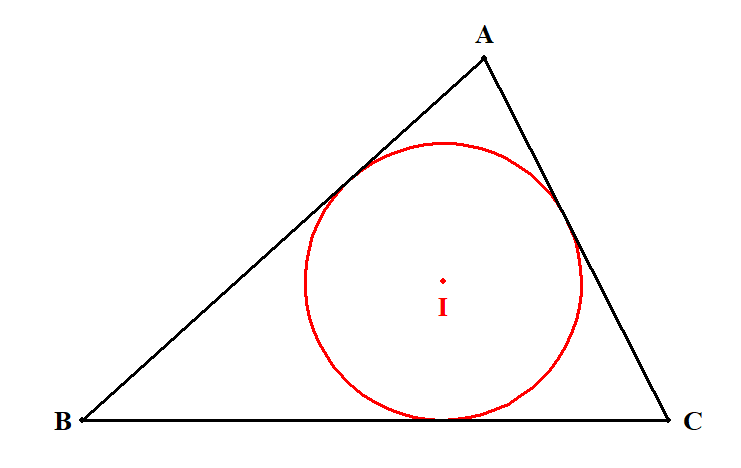
補足
「接する」とは
「接する」という言葉の意味については,何となく分かるとは思います。
詳しい説明は数学Ⅱで「微分」を学ぶまでできませんが,ふわっと説明をしておくと「またがずに触れるだけ」という感じです。
これから内接円の半径\(r\)を考えていきます。
下図のように,内心\(\mathrm{I}\)から円と三角形の接点に線分をひくと,線分の長さが\(r\)ですね。
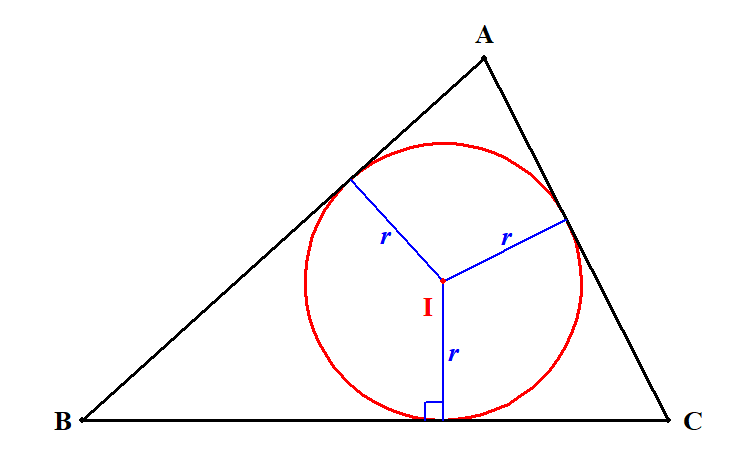
この線分は内接円の半径であり,三角形の辺の垂線になっています。
(接線が半径に垂直であることは,数学Aで学習します。)
したがって内接円の半径は,三角形の辺を底辺とする三角形の高さとして使えそうです。
そうすれば三角形の面積の問題に帰着できますね。
そのために,次のように内心\(\mathrm{I}\)から三角形の頂点に線分をひきます。
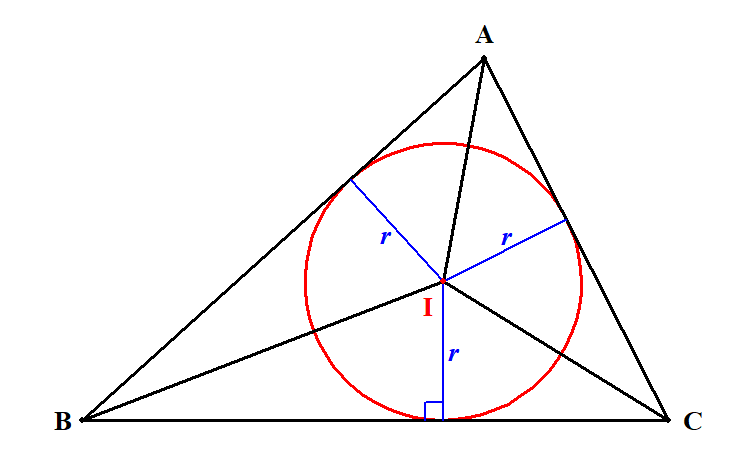
これで\(\triangle\mathrm{ABC}\)が,内接円の半径を高さとする3つの三角形に分割できたのですが,図がごちゃごちゃしてきて見づらいですね。
分割後の三角形のひとつ,\(\triangle\mathrm{IBC}\)に注目してみましょう。
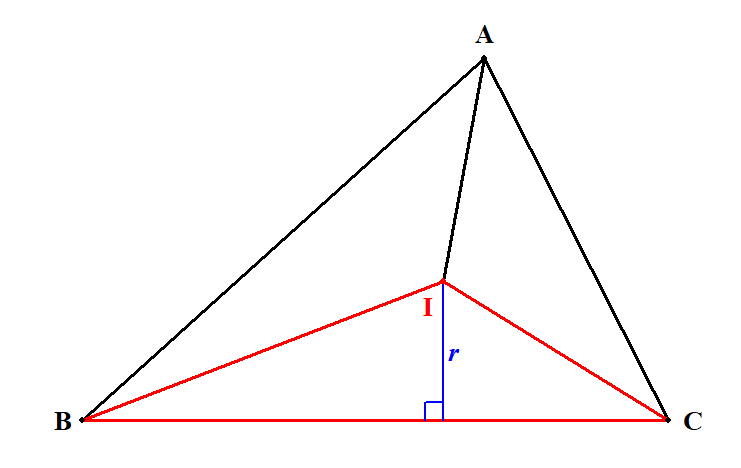
\(\triangle\mathrm{IBC}\)は辺\(\mathrm{BC}\)を底辺とし,内接円の半径を高さとする三角形です。
\(\mathrm{BC} = a\)ですから,その面積は次の式で表せます。
\(
\begin{align}
\triangle\mathrm{IBC} = \displaystyle\frac{1}{2}ar
\end{align}
\)
同様に\(\triangle\mathrm{ICA}\),\(\triangle\mathrm{IAB}\)の面積も分かります。
したがって,\(\triangle\mathrm{ABC}\)の面積を\(S\)とすると,次が成り立ちます。
\(
\begin{align}
\triangle\mathrm{ABC} &= \triangle\mathrm{IBC} + \triangle\mathrm{ICA} + \triangle\mathrm{IAB} \\[5pt]
S &= \displaystyle\frac{1}{2}ar + \displaystyle\frac{1}{2}br + \displaystyle\frac{1}{2}cr \\[5pt]
S &= \displaystyle\frac{a + b + c}{2}r \\[5pt]
r &= \displaystyle\frac{2S}{a + b + c}
\end{align}
\)
これで三角形の内接円の半径の求め方が分かりましたが,これは公式として覚えるようなものではありません。
次の点を押さえておけば,自然と解法も分かるでしょう。
- 内接円の半径は,三角形の辺と垂直である
- 内心と三角形の頂点を結ぶと,3つの三角形に分割できる
- 分割後の三角形は,内接円の半径を高さとする三角形になる
- 分割後の三角形の面積を合わせると,元の三角形の面積になる
確認問題
\(a = 4\),\(b = 5\),\(c = 6\)である\(\triangle\mathrm{ABC}\)について,外接円の半径\(R\)と内接円の半径\(r\)を求めてください。
答え
外接円の半径は,正弦定理で求められます。
内接円の半径は,三角形の面積に注目すれば求められます。
どちらにしても\(\sin\)の値が必要ですね。
角度が1つも分かっていませんが,3辺の長さが分かっていますから,余弦定理により\(\cos\)の値を求められます。
\(
\begin{align}
\cos A &= \displaystyle\frac{b^2 + c^2 - a^2}{2bc} \\[5pt]
&= \displaystyle\frac{5^2 + 6^2 - 4^2}{2 \cdot 5 \cdot 6} \\[5pt]
&= \displaystyle\frac{25 + 36 - 16}{60} \\[5pt]
&= \displaystyle\frac{45}{60} \\[5pt]
&= \displaystyle\frac{3}{4}
\end{align}
\)
\(0^{\circ} < A < 180^{\circ}\)なので\(\sin A > 0\)ですから,\(\sin A\)が求められます。
\(
\begin{align}
\sin ^2 A + \cos^2 A &= 1 \\[5pt]
\sin^2 A &= 1 - \cos^2 A \\[5pt]
&= 1 - \left(\displaystyle\frac{3}{4}\right)^2 \\[5pt]
&= 1 - \displaystyle\frac{9}{16} \\[5pt]
&= \displaystyle\frac{7}{16} \\[5pt]
\sin A &= \displaystyle\frac{\sqrt{7}}{4}
\end{align}
\)
これで正弦定理により,\(R\)が求められます。
\(
\begin{align}
2R &= \displaystyle\frac{a}{\sin A} \\[5pt]
&= \displaystyle\frac{4}{\displaystyle\frac{\sqrt{7}}{4}} \\[5pt]
&= 4 \cdot \displaystyle\frac{4}{\sqrt{7}} \\[5pt]
&= \displaystyle\frac{16\sqrt{7}}{7} \\[5pt]
\textcolor{red}{R} &\textcolor{red}{=} \textcolor{red}{\displaystyle\frac{8\sqrt{7}}{7}}
\end{align}
\)
次に\(r\)を求めます。
内心\(\mathrm{I}\)から三角形の頂点に線分をひくと,下図のように\(\triangle\mathrm{ABC}\)は,内接円の半径を高さとする3つの三角形に分割されます。
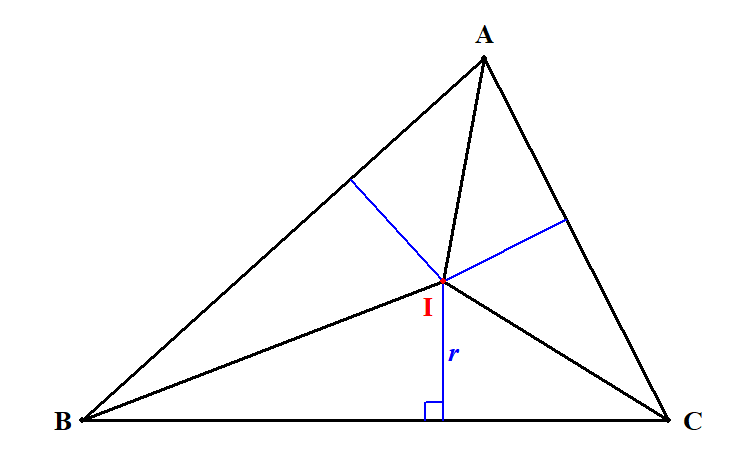
したがって,三角形の面積に注目すると,次の式が成り立ち,\(r\)が求められます。
\(
\begin{align}
\triangle\mathrm{ABC} &= \triangle\mathrm{IBC} + \triangle\mathrm{ICA} + \triangle\mathrm{IAB} \\[5pt]
\displaystyle\frac{1}{2}bc\sin A &= \displaystyle\frac{1}{2}ar + \displaystyle\frac{1}{2}br + \displaystyle\frac{1}{2}cr \\[5pt]
bc\sin A &= (a + b + c)r \\[5pt]
r &= \displaystyle\frac{bc}{a + b + c}\sin A \\[5pt]
&= \displaystyle\frac{5 \cdot 6}{4 + 5 + 6} \cdot \displaystyle\frac{\sqrt{7}}{4} \\[5pt]
&= \displaystyle\frac{30}{15} \cdot \displaystyle\frac{\sqrt{7}}{4} \\[5pt]
\textcolor{red}{r} &\textcolor{red}{=} \textcolor{red}{\displaystyle\frac{\sqrt{7}}{2}}
\end{align}
\)
\(\triangle\mathrm{ABC}\)の外接円の半径を\(R\),内接円の半径を\(r\)とするとき,次の式が成り立つことを証明してください。
\(
\begin{align}
2Rr = \displaystyle\frac{abc}{a + b + c}
\end{align}
\)
【ヒント】\(\triangle\mathrm{ABC}\)の面積は\(R\)で表すことも\(r\)で表すこともできます。
答え
問題にするような重要な式でも何でもありませんが,解いてみましょう。
外接円の半径と内接円の半径を結び付ける情報が必要ですが,ヒントの通り,\(\triangle\mathrm{ABC}\)の面積\(S\)に注目します。
まず\(\triangle\mathrm{ABC}\)の面積\(S\)を\(R\)で表します。
三角形の面積は\(\sin\)を使って求められました。
そして\(\sin\)は正弦定理で変形できます。
\(
\begin{align}
S &= \displaystyle\frac{1}{2}bc\sin A \\[5pt]
&= \displaystyle\frac{1}{2}bc \cdot \displaystyle\frac{a}{2R} \\[5pt]
&= \displaystyle\frac{abc}{4R}
\end{align}
\)
次に\(S\)を\(r\)で表します。
内心\(\mathrm{I}\)から三角形の頂点に線分をひくと,下図のように\(\triangle\mathrm{ABC}\)は,内接円の半径を高さとする3つの三角形に分割されます。

したがって,三角形の面積に注目すると,次の式が成り立ちます。
\(
\begin{align}
\triangle\mathrm{ABC} &= \triangle\mathrm{IBC} + \triangle\mathrm{ICA} + \triangle\mathrm{IAB} \\[5pt]
S &= \displaystyle\frac{1}{2}ar + \displaystyle\frac{1}{2}br + \displaystyle\frac{1}{2}cr \\[5pt]
&= \displaystyle\frac{a + b + c}{2}r
\end{align}
\)
上2つの式から,次の式が成り立ちます。
\(
\begin{align}
\displaystyle\frac{abc}{4R} &= \displaystyle\frac{a + b + c}{2}r \\[5pt]
2Rr &= \displaystyle\frac{abc}{a + b + c}
\end{align}
\)






