三角比は,直角三角形の辺の比です。 基本的な図形の計量を行う上で三角比は重要です。 曲線のない図形なら三角形に分割できるからですね。 応用はまた後で扱いますが,まずは基本だけ学びましょう。
目次
三角比
これから学ぶことを理解するため,まず中学校で学んだ直角三角形の相似条件を思い出しましょう。
- 直角以外の角度が1つ等しい
- 対応する2辺の比がそれぞれ等しい
ここで重要なのは1つめの相似条件です。 直角以外の角度が等しい直角三角形はすべて相似なのです。 つまり直角以外の角度をひとつ決めるだけで,2辺の比が自動的に決まるわけです。
下図のように,直角以外の角度のひとつを\(\theta\)としましょう。 また3辺の長さを\(a, b, c\)として,それらの比を考えてみましょう。
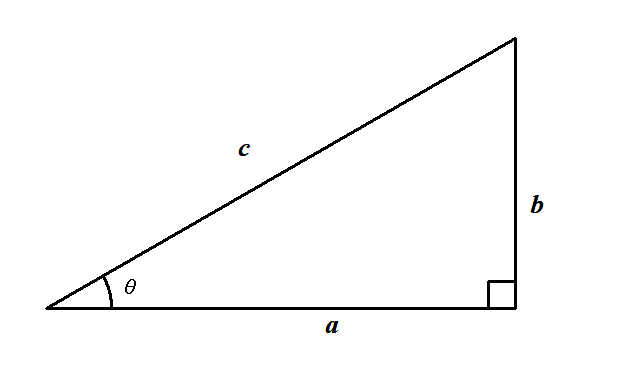
比には\(a, b\)の比,\(b, c\)の比,\(c, a\)の比の3種類があります。 これは\(\theta\)によって決まりますから,\(\theta\)の関数のように表すことができます。 それが次の三角比です。
上図の直角三角形において,3辺\(a, b, c\)の比は\(\theta\)によって決まる。 それを次のように表す。
- \(\sin\theta = \displaystyle\frac{b}{c}\)
- \(\cos\theta = \displaystyle\frac{a}{c}\)
- \(\tan\theta = \displaystyle\frac{b}{a}\)
\(\sin, \ \cos, \ \tan\)の読み方と日本語での言い方は次の通りです。
| 記号 | 読み方 | 日本語 |
|---|---|---|
| \(\sin\) | サイン\((\mathrm{sine})\) | 正弦 |
| \(\cos\) | コサイン\((\mathrm{cosine})\) | 余弦 |
| \(\tan\) | タンジェント\((\mathrm{tangent})\) | 正接 |
\(\sin, \ \cos, \ \tan\)は初めて見ると混乱しがちです。 それぞれ何分の何だったか思い出せるような定番の覚え方がありますので,紹介します。
それぞれの頭文字である\(\mathrm{s}, \ \mathrm{c}, \ \mathrm{t}\)の筆記体は次のような形です。

これを直角三角形の角に当てはめると次のようになります。
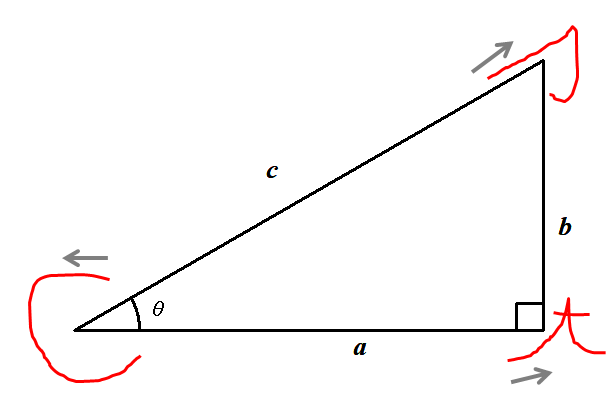
筆記体を書き順通りになぞってみてください。 \(\mathrm{s}\)をなぞると「\(c\)→\(b\)」と辺を通りますが,これは\(\sin\theta\)が「\(c\)分の\(b\)」であることと対応します。 同様に筆記体の\(c\)をなぞると\(\cos\theta\)が「\(c\)分の\(a\)」であることが,\(t\)をなぞると\(\tan\theta\)が「\(a\)分の\(b\)」であることが分かります。
これでいくらか覚えやすくなりますね。
先ほど直角三角形の辺を\(a, b, c\)と表しましたが,実は日本語の名前も付いています。 (覚える必要はありません。)
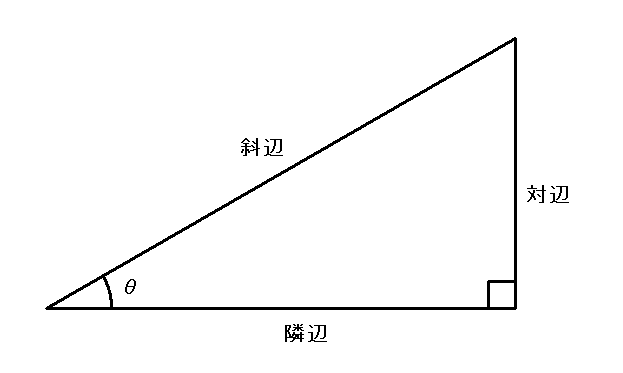
直角の向かい側の辺を「斜辺」というのは知っていますね。 角度\(\theta\)の角をはさむ2辺のうち,斜辺じゃない方を「隣辺」といいます。 また,角度\(\theta\)の角の向かい側の辺のことを「対辺」といいます。
\(\sin, \ \cos, \ \tan\)の定義では\(\displaystyle\frac{b}{c}\),\(\displaystyle\frac{a}{c}\),\(\displaystyle\frac{b}{a}\)という比のとり方をしました。 もちろん分母分子を逆にした比のとり方も考えられて,次のように定義されています。 (覚える必要はありません。)
\(\sec\)はセカント\((\mathrm{secant})\)と読み,日本語では正割といいます。 \(\csc\)は\(\mathrm{cosec}\)とも書き,コセカント\((\mathrm{cosecant})\)と読み,日本語では余割といいます。 \(\cot\)はコタンジェント\((\mathrm{cotangent})\)と読み,日本語では余接といいます。
三角比の代表的な値
直角三角形の3辺の比は,\(\theta\)が\(30^{\circ}\),\(45^{\circ}\),\(60^{\circ}\)のときの値がよく知られています。 このときの3辺の比は,下図の通りです。
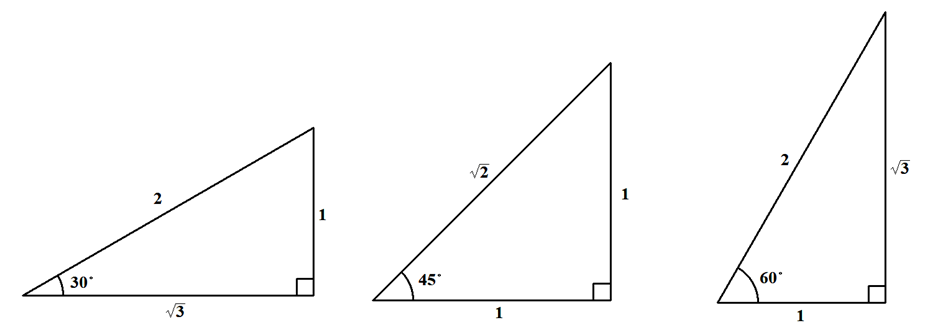
\(\theta = 30^{\circ}\)の直角三角形は,1辺が\(2\)の正三角形を半分にしたものになっています。 半分に分かれた辺の長さは\(1\)になり,残りの辺は三平方の定理から\(\sqrt{3}\)になると分かります。 \(\theta = 60^{\circ}\)の場合も同じです。
\(\theta = 45^{\circ}\)の直角三角形は,残り1つの角度も\(45^{\circ}\)で二等辺三角形になります。 よって,直角をはさむ2辺の長さは同じであり,それを\(1\)とすると,残りの1辺は三平方の定理により\(\sqrt{2}\)になると分かります。
この図から,\(\theta\)が\(30^{\circ}\),\(45^{\circ}\),\(60^{\circ}\)のときの\(\sin\theta\),\(\cos\theta\),\(\tan\theta\)の値が分かります。
| \(\theta\) | \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
|---|---|---|---|
| \(30^{\circ}\) | \(\displaystyle\frac{1}{2}\) | \(\displaystyle\frac{\sqrt{3}}{2}\) | \(\displaystyle\frac{1}{\sqrt{3}}\) |
| \(45^{\circ}\) | \(\displaystyle\frac{1}{\sqrt{2}}\) | \(\displaystyle\frac{1}{\sqrt{2}}\) | \(1\) |
| \(60^{\circ}\) | \(\displaystyle\frac{\sqrt{3}}{2}\) | \(\displaystyle\frac{1}{2}\) | \(\sqrt{3}\) |
この値は非常によく使います。 丸暗記の必要はありませんが,直角三角形の3辺の比は思い出せるようにしておきましょう。 3辺の比さえ分かれば,三角比も分かるからです。
\(\theta\)が上記以外の値のときは,簡単には三角比の値を求められません。 今は\(30^{\circ}\),\(45^{\circ}\),\(60^{\circ}\)の三角比の値さえ分かればOKです。
三角比の使い方
いきなり三角比というものが登場しましたが,まだ使い道が分かりませんね。 ざっくりいうと,三角比には,角度を頼りに辺の長さを変換する機能があります。 (今のところ直角三角形だけですが)
先ほどの補足にあった下図を見てください。

先ほどは三角比が何分の何なのかを覚えるために使った図ですが,辺の変換の仕方を示す図としても使えます。 次のような辺の変換ができるのです。
つまり,\(\sin\theta\)は「\(c\)→\(b\)」と変換する道具でもあるわけです。 \(\cos\theta\),\(\tan\theta\)も同様です。
今回学んだ範囲ではこの程度の使い道しかありませんが,今後どんどん応用範囲が広がっていきます。 いきなり\(\sin\),\(\cos\),\(\tan\)と記号が増えて嫌かもしれませんが,今のうちに慣れておきましょう。
確認問題
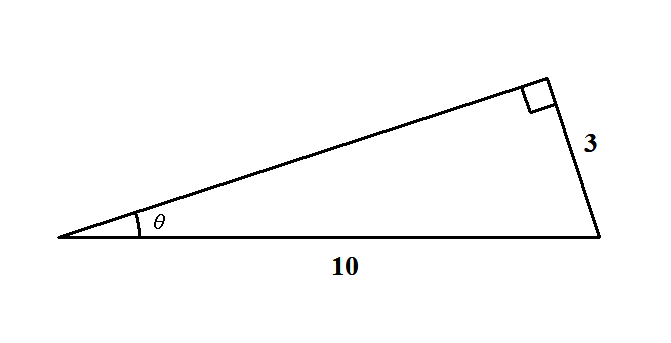
次の図で\(\sin\theta\),\(\cos\theta\),\(\tan\theta\)を求めてください。
答え
まずは3辺の長さをはっきりさせましょう。 1辺の長さが与えられていませんが,これを\(x\)とすると,\(x\)は三平方の定理で求められます。
3辺の長さが分かってしまえば,あとは比をとるだけで三角比が求められます。 どことどこの比をとるのか間違えないよう,図形を回転・反転させておきます。
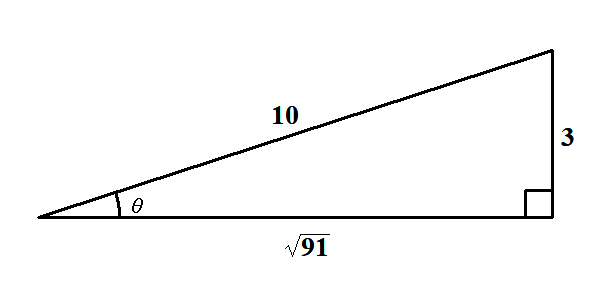
この図から,三角比が次のように求められます。
次の図で\(\tan\theta = \displaystyle\frac{5}{7}\)とします。 直角三角形の斜辺の長さと\(\cos\theta\)を求めてください。
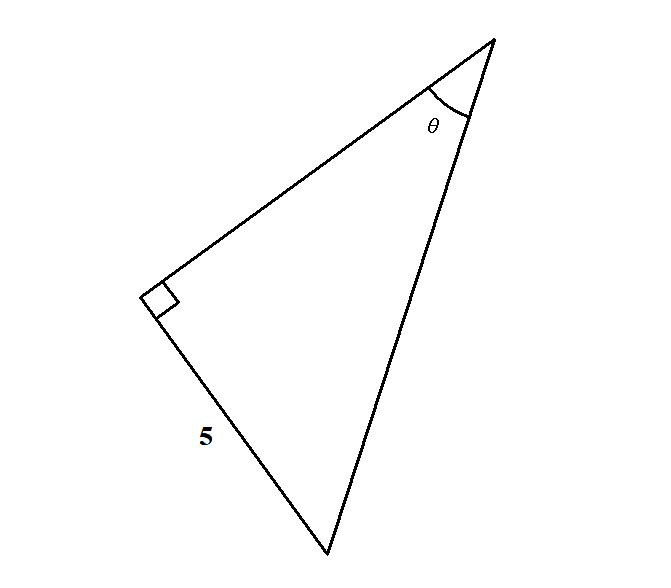
答え
\(\tan\theta\)の情報を活用したいですが,まだ三角比に慣れていないと思うので,見やすいように図を回転させておきます。 また,長さが分かっていない辺の長さを下図のように\(x, y\)とおきます。
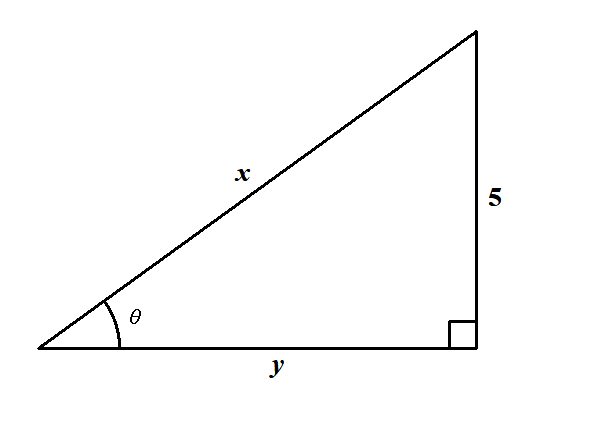
今分かっている情報は,1辺の長さが\(5\)であることと\(\tan\theta\)の値だけですから,これを活用します。 \(\tan\theta\)が何の比であったかを思い出すと,次のように\(y\)を求められます。
したがって,斜辺の長さ\(x\)は三平方の定理により次のように求められます。
したがって,\(\cos\theta\)も次のように求められます。
\(\theta\)が\(15^{\circ}\),\(18^{\circ}\)のときの三角比について,次の値が分かっています。
| \(\theta\) | \(\sin\theta\) | \(\cos\theta\) |
|---|---|---|
| \(15^{\circ}\) | \(\displaystyle\frac{\sqrt{6} - \sqrt{2}}{4}\) | \(\displaystyle\frac{\sqrt{6} + \sqrt{2}}{4}\) |
| \(18^{\circ}\) | \(\displaystyle\frac{\sqrt{5} - 1}{4}\) | \(\displaystyle\frac{\sqrt{10 + 2\sqrt{5}}}{4}\) |
この値を利用して,次の図の\(x\)を求めてください。
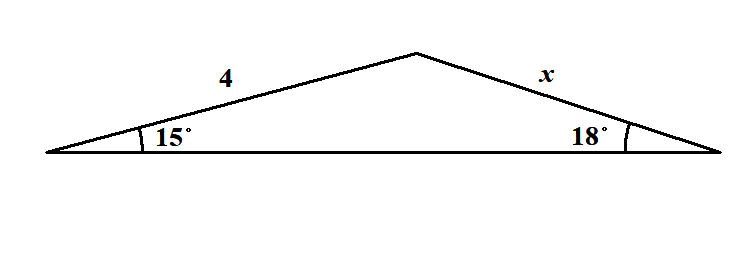
答え
\(15^{\circ}\),\(18^{\circ}\)の三角比を利用するため,直角三角形をつくります。 \(15^{\circ}\)でも\(18^{\circ}\)でもない角から向かいの辺に垂線を引くと,それぞれ\(15^{\circ}\),\(18^{\circ}\)の角をもつ2つの直角三角形に分割できます。

上図では垂線の長さを\(h\)とおいています。 これは両者の三角形に共通する辺であり,両者を繋ぐ情報として利用できます。
\(15^{\circ}\)の角をもつ方の三角形では1辺の長さが分かっているため,これを利用して\(h\)が求められます。 \(\sin 15^{\circ}\)を使えば辺の長さを変換できますね。
次にこの\(h\)の情報をもう一方の三角形に引き継ぐことで,\(x\)を求めます。 \(x\)と\(h\)を繋ぐには,\(\sin 18^{\circ}\)を利用できますね。
