図形と計量第 6 回

正弦定理

◀

三角比を含む不等式

余弦定理

▶

はじめに

三角比は元々，直角三角形という図形に関するものでしたが，三角比を拡張して以来，何だか図形の話から遠ざかった気がしますね。 今回からは，また三角比を図形の問題に応用していきます。

目次

正弦定理

▼

前回までの学習で，三角比の扱いには慣れてきたと思います。 しかし，三角比の計算ができるだけでは役に立ちません。 図形の問題に応用できるので，確認していきましょう。

まずは正弦定理を学びます。 これは三角形の辺とその対角の関係を表すものです。 以後，次のような三角形\(\mathrm{ABC}\)を使って話を進めていきます。

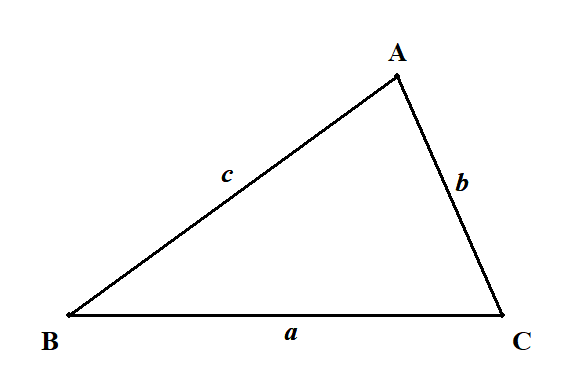
\(\triangle \mathrm{ABC}\)において，頂点\(\mathrm{A}\)，\(\mathrm{B}\)，\(\mathrm{C}\)の向かい側の辺の長さをそれぞれ\(a\)，\(b\)，\(c\)としています。 また，\(\angle \mathrm{A}\)，\(\angle \mathrm{B}\)，\(\angle \mathrm{C}\)の大きさを\(A\)，\(B\)，\(C\)とします。

それでは，正弦定理の内容を確認してみましょう。

正弦定理

\(\triangle \mathrm{ABC}\)の外接円の半径を\(R\)とすると，次の関係式が成り立つ。

\( \begin{align} \displaystyle\frac{a}{\sin A} = \displaystyle\frac{b}{\sin B} = \displaystyle\frac{c}{\sin C} = 2R \end{align} \)

三角形の外接円というのは，三角形の３つの頂点をすべて通る円のことです。 図にすると次のような感じで，三角形に外側から接する円です。

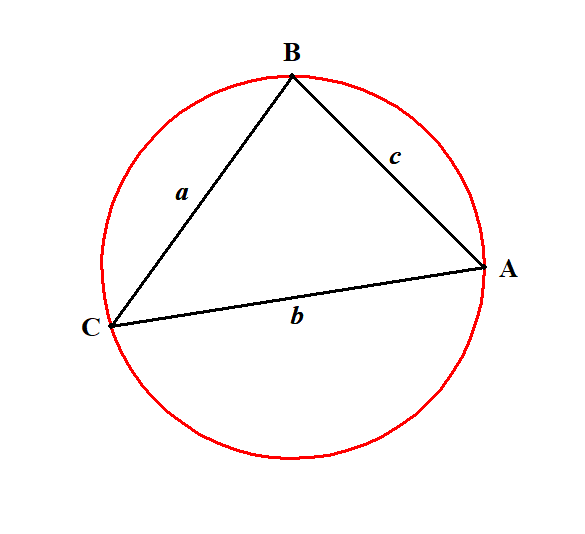
外接円はどんな三角形にもただ１つだけ存在し，正弦定理はどんな三角形に対しても成り立ちます。 次項で証明を確認してから，次々項でどんな風に使えるか見てみます。

正弦定理の証明

▲
▼

正弦定理を使う前に，ちゃんと証明しておきましょう。

\(\displaystyle\frac{a}{\sin A} = \displaystyle\frac{b}{\sin B}\)といった関係を証明するだけなら簡単です。 次のように角\(\mathrm{C}\)から対辺に垂線\(\mathrm{CH}\)を下ろします。 三角比を使うために直角三角形をつくるわけですね。

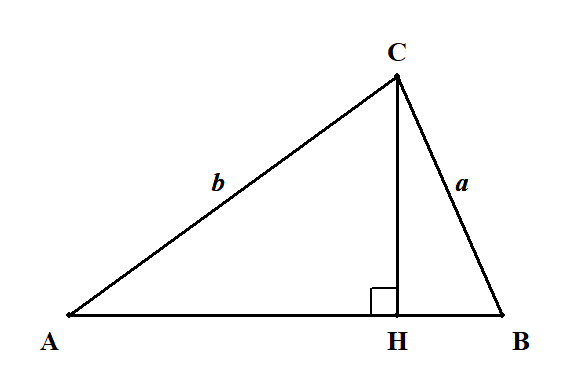
２つの直角三角形ができましたが，辺\(\mathrm{CH}\)が共通なので，そこから関係式を導きましょう。 左側の直角三角形から次の式が得られます。

\( \begin{align} \mathrm{CH} = b \sin A \end{align} \)

また，右側の直角三角形から次の式が得られます。

\( \begin{align} \mathrm{CH} = a \sin B \end{align} \)

これらの式から，次のように正弦定理の式が得られます。

\( \begin{align} a \sin B &= b \sin A \\[5pt] \displaystyle\frac{a}{\sin A} &= \displaystyle\frac{b}{\sin B} \end{align} \)

次に\(\displaystyle\frac{a}{\sin A} = 2R\)といった関係式を証明してみましょう。 少し形を変えて\(a = 2R \sin A\)とすると，この式は円の直径を斜辺とする直角三角形の三角比の式っぽいですね。

証明の方針は，直径を斜辺とする直角三角形をつくることです。 角\(\mathrm{A}\)が直角・鋭角・鈍角の場合に分けて考えます。

証明中，図形の性質を色々利用しますが，それについては数学Ａで詳しく解説します。

[1] 角\(\mathrm{A}\)が直角の場合

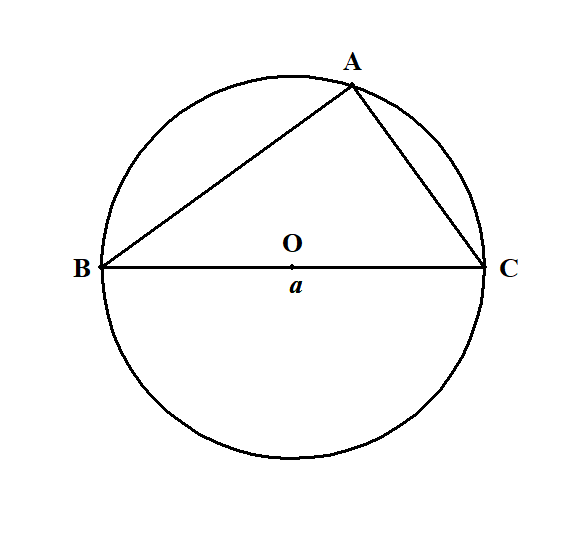
このとき，図のように対辺は外接円の直径になります。 したがって，次の式が成り立ちます。

\( \begin{align} a &= 2R \\[5pt] &= 2R\sin90^{\circ} \\[5pt] &= 2R\sin A \end{align} \)
補足 タレスの定理

中学で学びましたが，直径に対する円周角は直角になります。 これをタレスの定理といいます。

タレスの定理の逆も成り立ちます。 つまり，上図のように直角三角形の斜辺は，外接円の直径になります。 本文の説明ではこのことを使っています。

[2] 角\(\mathrm{A}\)が鋭角の場合

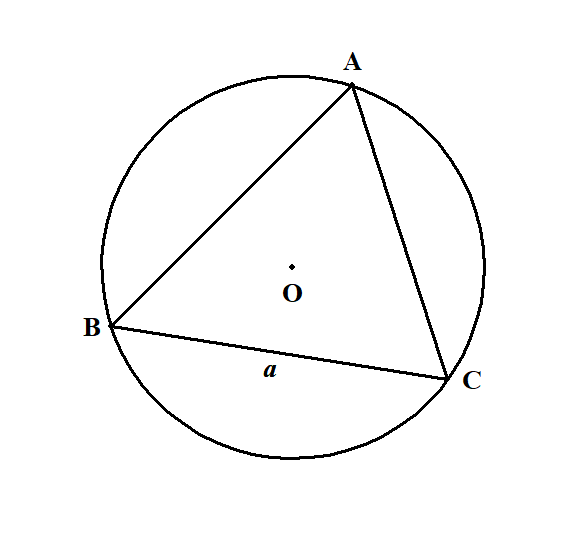
このとき，上図のように外接円の中心は，三角形の内部にあります。 円の直径を利用した方が考えやすいので，次図のように点\(\mathrm{D}\)をとってみます。 \(\mathrm{BD}\)が直径になるようにするのです。 また，円周角の定理により，\(\angle \mathrm{D} = \angle \mathrm{A}\)ですね。

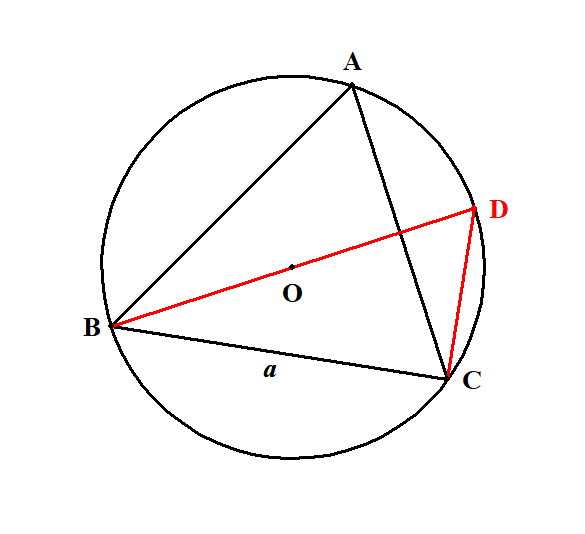
タレスの定理により，\(\angle \mathrm{BCD} = 90^{\circ}\)ですから，\(\triangle \mathrm{BCD}\)は直角三角形です。 したがって，次の式が成り立ちます。

\( \begin{align} a &= \mathrm{BD} \sin D \\[5pt] &= 2R \sin A \end{align} \)

[3] 角\(\mathrm{A}\)が鈍角の場合

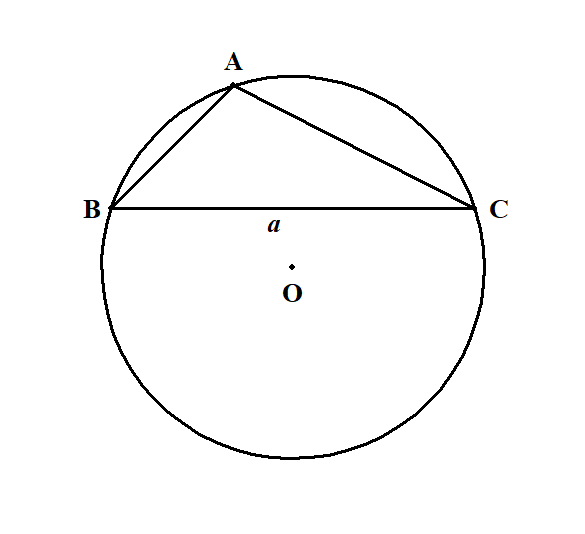
このとき，上図のように外接円の中心は，三角形の外部にあります。 先ほどと全く同じように，\(\mathrm{BD}\)が直径となるように点\(\mathrm{D}\)をとります。

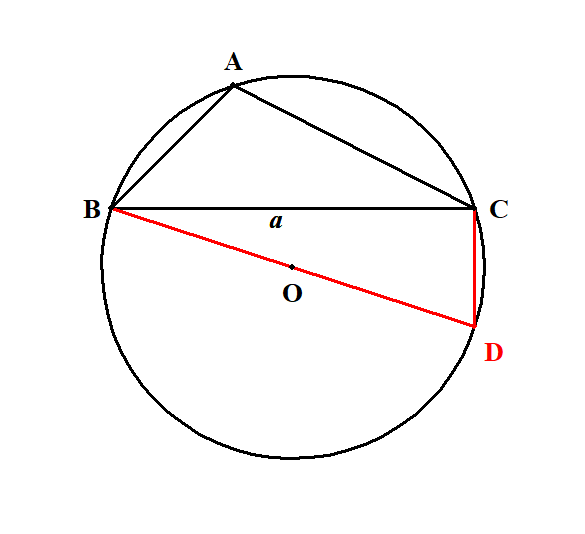
詳しくは数学Ａで学びますが，円に内接する四角形の対角の和は\(180^{\circ}\)です。 したがって，補角の公式も使うと，次の式が成り立ちます。

\( \begin{align} a &= \mathrm{BD} \sin D \\[5pt] &= 2R \sin (180^{\circ} - A) \\[5pt] &= 2R \sin A \end{align} \)

以上の[1]，[2]，[3]より，正弦定理が成り立つことが証明できました。

正弦定理の使い方

▲
▼

正弦定理を使えば，ある角の角度が分かればその対辺の長さが分かり，ある辺の長さが分かればその対角の角度が分かります。

ただしその計算を進めるには，他の角とその対辺のペアが分かっているか，外接円の半径が分かっている必要があります。 例をひとつ見てみましょう。 次の図で辺\(\mathrm{AB}\)の長さを求めてみます。

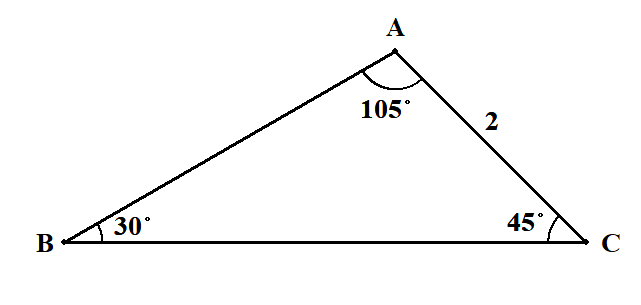
正弦定理を使えば，次のように簡単に計算できます。

\( \begin{align} \displaystyle\frac{\mathrm{AB}}{\sin C} &= \displaystyle\frac{\mathrm{CA}}{\sin B} \\[5pt] \mathrm{AB} &= \displaystyle\frac{\mathrm{CA}}{\sin B} \cdot \sin C \\[5pt] &= \displaystyle\frac{2}{\sin 30^{\circ}} \cdot \sin 45^{\circ} \\[5pt] &= \displaystyle\frac{2}{\displaystyle\frac{1}{2}} \cdot \displaystyle\frac{1}{\sqrt{2}} \\[5pt] &= 2\sqrt{2} \end{align} \)

確認問題でもう少し練習しておきましょう。

補足 繁分数の整理

正弦定理の計算をしていると，分数の分母や分子にさらに分数が登場することがあります。 これを繁分数というのですが，ちょっと見慣れない形ですから，計算方法を確認しておきましょう。

次の繁分数を整理します。

\( \begin{align} \displaystyle\frac{\displaystyle\frac{5}{14}}{\displaystyle\frac{10}{21}} \end{align} \)

主な計算方法は２種類あります。

ひとつめは，一度割り算の形に直すことです。 だいぶ見やすくなります。

\( \begin{align} \displaystyle\frac{\displaystyle\frac{5}{14}}{\displaystyle\frac{10}{21}} &= \displaystyle\frac{5}{14} \div \displaystyle\frac{10}{21} \\[5pt] &= \displaystyle\frac{5}{14} \cdot \displaystyle\frac{21}{10} \\[5pt] &= \displaystyle\frac{3}{4} \end{align} \)

ふたつめは，分母分子に同じ数をかけて整理する方法です。 分母・分子中にある分数の分母を払うようにします。 言葉で書くとややこしいので，とにかく具体例を見ましょう！

\( \begin{align} \displaystyle\frac{\displaystyle\frac{5}{14}}{\displaystyle\frac{10}{21}} &= \displaystyle\frac{\displaystyle\frac{5}{14} \times 42}{\displaystyle\frac{10}{21} \times 42} \\[5pt] &= \displaystyle\frac{15}{20} \\[5pt] &= \displaystyle\frac{3}{4} \end{align} \)

確認問題

▲

次の三角形で角度\(x\)と外接円の半径\(R\)を求めてください。 図の角\(\mathrm{A}\)の大きさは仮のものなので，見た目での判断は厳禁です。

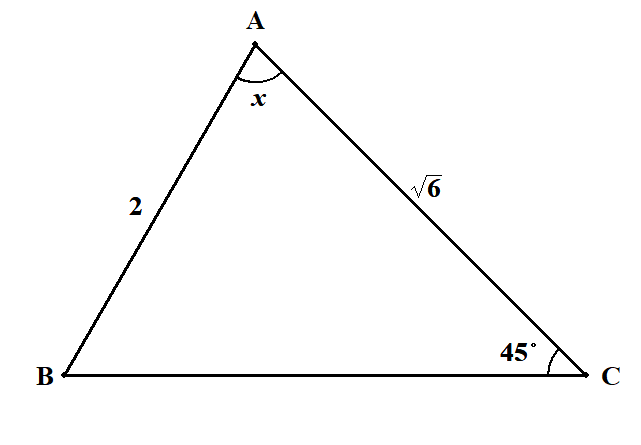
答え

辺とその対角の情報がペアでそろっていれば，正弦定理が有効です。 辺\(\mathrm{AB}\)と角\(\mathrm{C}\)のペアが分かっているので，まず\(R\)を求めてしまいましょう。

\( \begin{align} 2R &= \displaystyle\frac{2}{\sin 45^{\circ}} \\[5pt] R &= \displaystyle\frac{2}{\displaystyle\frac{1}{\sqrt{2}}} \cdot \displaystyle\frac{1}{2} \\[5pt] \textcolor{red}{R} &\textcolor{red}{=} \textcolor{red}{\sqrt{2}} \end{align} \)

\(x\)については，対辺が分からないので，すぐには求められません。 まずは\(B\)の方を求めます。

\( \begin{align} \displaystyle\frac{\sqrt{6}}{\sin B} &= 2R \\[5pt] \sin B &= \displaystyle\frac{\sqrt{6}}{2R} \\[5pt] &= \displaystyle\frac{\sqrt{6}}{2\sqrt{2}} \\[5pt] &= \displaystyle\frac{\sqrt{3}}{2} \\[5pt] B &= 60^{\circ}, \ 120^{\circ} \end{align} \)

\(B\)としてありえる角度は\(60^{\circ}\)，\(120^{\circ}\)の２つがあります。 鈍角の可能性も忘れないでください。

\(x\)は残りの角の角度ですから，\(x = 75^{\circ}, \ 15^{\circ}\)です。 条件を満たすような三角形は２つあったわけです。

次の図で点\(\mathrm{O}\)は\(\triangle \mathrm{ABC}\)の外接円の中心です。 辺\(\mathrm{AB}\)，辺\(\mathrm{CA}\)の長さを求めてください。

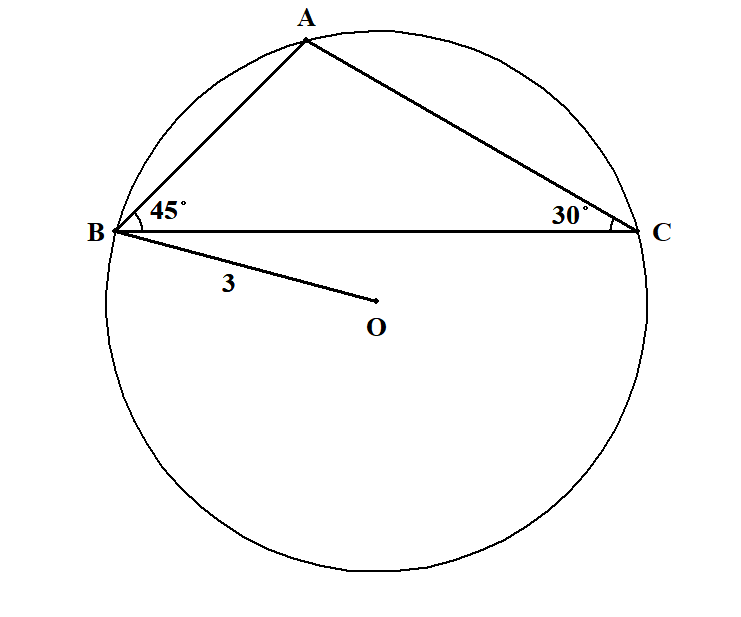
答え

三角形と外接円の組み合わせを扱うときは，正弦定理が役立ちます。 まず\(\mathrm{AB}\)を求めましょう。

\( \begin{align} \displaystyle\frac{\mathrm{AB}}{\sin 30^{\circ}} &= 2 \cdot 3 \\[5pt] \mathrm{AB} &= 6 \sin 30^{\circ} \\[5pt] \mathrm{AB} &= 6 \cdot \displaystyle\frac{1}{2} \\[5pt] \textcolor{red}{\mathrm{AB}} &\textcolor{red}{=} \textcolor{red}{3} \end{align} \)

次に\(\mathrm{CA}\)を求めましょう。

\( \begin{align} \displaystyle\frac{\mathrm{CA}}{\sin 45^{\circ}} &= 2 \cdot 3 \\[5pt] \mathrm{CA} &= 6 \sin 45^{\circ} \\[5pt] \mathrm{CA} &= 6 \cdot \displaystyle\frac{1}{\sqrt{2}} \\[5pt] \textcolor{red}{\mathrm{CA}} &\textcolor{red}{=} \textcolor{red}{3\sqrt{2}} \end{align} \)

１辺の長さが\(a\)である正三角形の外接円の面積を求めてください。

答え

いろいろな方法で解けると思いますが，せっかくなので正弦定理を使いましょう。 求める面積を\(S\)とします。

外接円の半径を\(R\)とすると，正弦定理により，\(R\)は次のように求められます。

\( \begin{align} 2R &= \displaystyle\frac{a}{\sin 60^{\circ}} \\[5pt] R &= \displaystyle\frac{a}{\displaystyle\frac{\sqrt{3}}{2}} \cdot \displaystyle\frac{1}{2} \\[5pt] &= a \cdot \displaystyle\frac{2}{\sqrt{3}} \cdot \displaystyle\frac{1}{2} \\[5pt] &= \displaystyle\frac{a}{\sqrt{3}} \end{align} \)

外接円の半径が分かりましたから，面積も分かります。

\( \begin{align} S &= \pi R^2 \\[5pt] S &= \pi \left(\displaystyle\frac{a}{\sqrt{3}}\right)^2 \\[5pt] \textcolor{red}{S} &\textcolor{red}{=} \textcolor{red}{\displaystyle\frac{1}{3}\pi a^2} \end{align} \)