正弦定理に引き続き,今回は余弦定理を学びます。 三角比を使って三平方の定理を拡張したものです。
目次
余弦定理
前回は正弦定理を学びました。 図形の問題に三角比,特に\(\sin\)を応用できるものでしたね。 今回はもうひとつ,\(\cos\)を活用する余弦定理を学びます。
余弦定理は三平方の定理の拡張版です。 前回同様,次のような三角形\(\mathrm{ABC}\)を使って話を進めていきます。
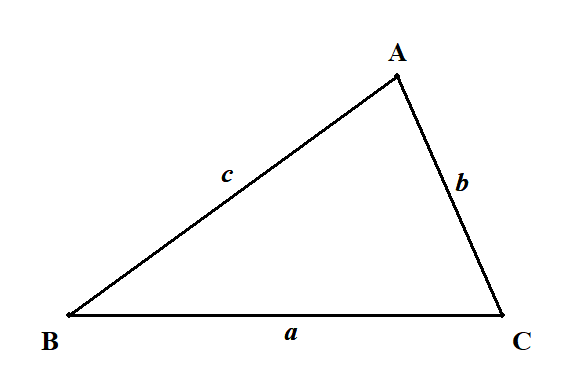
\(\triangle \mathrm{ABC}\)において,頂点\(\mathrm{A}\),\(\mathrm{B}\),\(\mathrm{C}\)の向かい側の辺の長さをそれぞれ\(a\),\(b\),\(c\)としています。 また,\(\angle \mathrm{A}\),\(\angle \mathrm{B}\),\(\angle \mathrm{C}\)の大きさを\(A\),\(B\),\(C\)とします。
それでは,余弦定理の内容を確認してみましょう。
\(\triangle \mathrm{ABC}\)について,次の関係式が成り立つ。
- \(a^2 = b^2 + c^2 - 2bc \cos A\)
- \(b^2 = c^2 + a^2 - 2ca \cos B\)
- \(c^2 = a^2 + b^2 - 2ab \cos C\)
長い式だなあ,と思うかもしれませんが,そんなに難しい式ではありません。 三平方の定理にちょっと付け足した式になっています。 右辺の最後の項がそれですね。
実際,例えば\(A = 90^{\circ}\)のとき,\(\cos A = 0\)ですから,1つめの式は次のようになります。
これはまさに\(\angle \mathrm{A}\)を直角とする直角三角形に対する三平方の定理です。 三平方の定理は,余弦定理の特別な場合なんですね。
余弦定理の証明
まずはちゃんと定理を証明しましょう。 先ほどの\(\triangle \mathrm{ABC}\)の図で,頂点\(\mathrm{A}\)から対辺に垂線\(\mathrm{AH}\)を下ろします。 直角三角形をつくるためです。
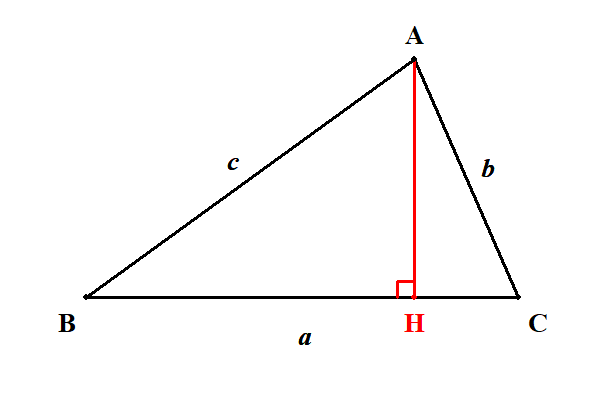
直角三角形\(\mathrm{ABH}\)ができたので,三平方の定理を使ってみます。
もうひとつ直角三角形\(\mathrm{CAH}\)ができていますね。 これを使えば\(\mathrm{AH}\),\(\mathrm{BH}\)が求められます。
これで先ほどの式の計算が続けられます。
これは余弦定理の3つめの式ですが,他の2つも全く同じように証明できます。
ところで,この証明が不十分であることには気づきましたか? \(\angle C\)が鋭角であることを前提とした式の立て方をしているのです。 直角の場合は三平方の定理なのでOKですが,鈍角の場合については証明できていません。
もし\(\angle C\)が鈍角なら点\(H\)の位置が変わり,式の立て方が変わります。 この場合の証明については確認問題としておきます。 やってみましょう。
余弦定理の使い方
余弦定理は三平方の定理の拡張版です。 三平方の定理では,直角三角形の2辺の長さが分かれば,残りの辺の長さが分かりました。 余弦定理も似たような使い方です。
余弦定理でも2辺の長さが分かれば,残りの辺の長さを求める手掛かりになります。 しかし三平方の定理が「直角」という情報を必要とするように,余弦定理でも対角の情報が必要です。
次の\(\triangle \mathrm{ABC}\)で\(x\)を求めてみましょう。
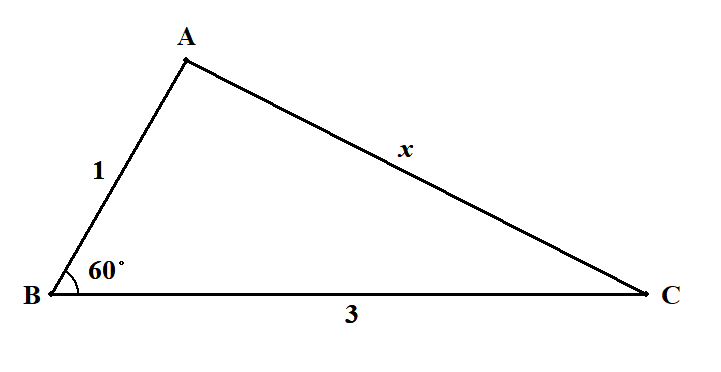
\(\angle \mathrm{B}\)が直角なら三平方の定理で一発でしたね。 今回は\(\angle \mathrm{B}\)が直角じゃないですが,このときは余弦定理で一発です。
\(x\)は辺の長さであり,もちろん正ですから,\(x = \sqrt{7}\)ですね。 このように,大体の使い方は三平方の定理と同じです。
余弦定理は辺の長さだけでなく,角度を求めるためにも使えます。 余弦定理の式を少し変形してみましょう。
\(\triangle \mathrm{ABC}\)について,次の関係式が成り立つ。
- \(\cos A = \displaystyle\frac{b^2 + c^2 - a^2}{2bc}\)
- \(\cos B = \displaystyle\frac{c^2 + a^2 - b^2}{2ca}\)
- \(\cos C = \displaystyle\frac{a^2 + b^2 - c^2}{2ab}\)
これは余弦定理の式を変形しただけですから,改めて丸暗記する必要はありません。
これを利用することで,3辺の長さが分かれば三角形のどの角についても\(\cos\)の値を求められます。 確認問題で練習してみましょう。
確認問題
本文では\(\angle \mathrm{C}\)が鋭角の場合について,次の余弦定理の式を証明しました。
\(\angle \mathrm{C}\)が直角の場合もこの式は成り立ちます。 ちょうど三平方の定理と同じになりますね。
あと証明できていないのは,\(\angle \mathrm{C}\)が鈍角の場合です。 このときにも余弦定理の式が成り立つことを証明してください。
答え
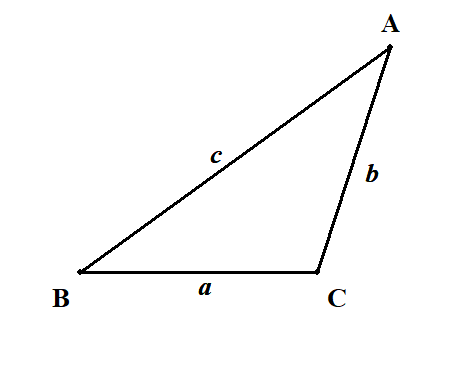
鋭角の場合と同じように,角\(\mathrm{A}\)から辺\(\mathrm{BC}\)の延長線上に垂線\(\mathrm{AH}\)を下ろします。 直角三角形をつくるわけですね。
直角三角形\(\mathrm{ABH}\)ができたので,三平方の定理を使ってみます。
もうひとつ直角三角形\(\mathrm{CAH}\)ができていますね。 これを使えば\(\mathrm{AH}\),\(\mathrm{BH}\)が求められます。 \(\angle \mathrm{ACH} = 180^{\circ} - C\)であることに注意してください。
これで先ほどの式の計算が続けられます。 途中の計算は,本文のものと完全に同じなので省略します。
これで\(\angle C\)が鈍角の場合も余弦定理が成り立つことが証明できました。
\(\triangle \mathrm{ABC}\)について,次の問いに答えてください。 辺の長さや角度の表し方については,本文の通りです。
-
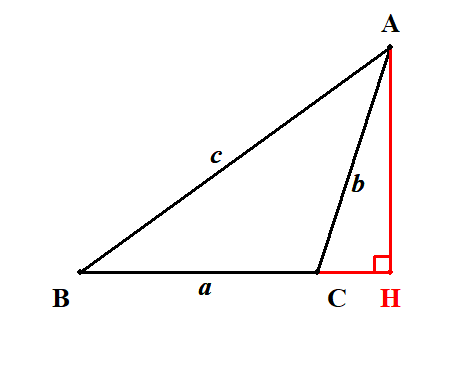
\(A = 45^{\circ}\),\(b = \sqrt{2}\),\(c = 5\)のとき,\(a\)を求めてください。
-
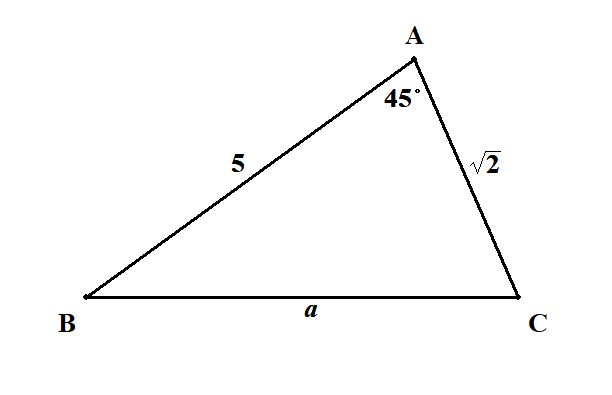
\(C = 120^{\circ}\),\(a = 2\),\(c = \sqrt{19}\)のとき,\(b\)を求めてください。
-
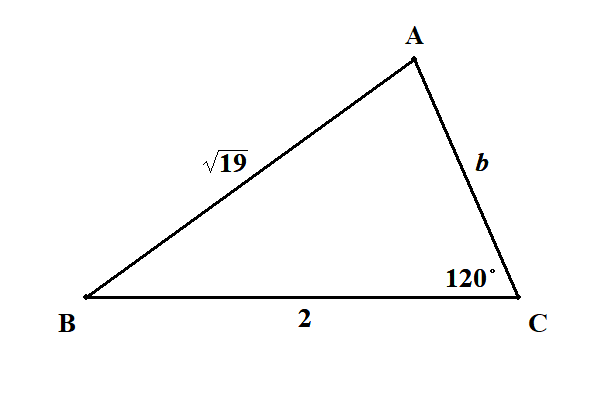
\(a = 3\),\(b = \sqrt{5}\),\(c = \sqrt{2}\)のとき,\(B\)を求めてください。
-
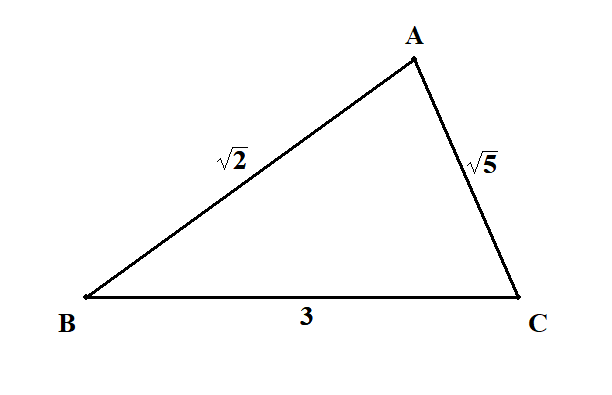
\(a = 2\),\(b = 3\),\(c = 4\)のとき,\(\cos C\)を求めてください。また,\(\angle C\)が鋭角・直角・鈍角のうちどれか答えてください。
答え
辺の長さが2つ,角度が1つ,これだけの情報があれば,余弦定理を使って残りの辺の長さが分かります。 また,3辺の長さが分かれば,余弦定理を使って好きな角の\(\cos\)の値が分かります。
余弦定理は,ある角が鋭角・直角・鈍角のどれか,ということを気にすることなく使えます。 なので正確な図がどうなるかは気にせず,適当な三角形の図をかいて情報を整理しましょう。
-
問題の三角形の情報を適当な図にまとめます。
\(\angle \mathrm{A}\)の情報を活用できるように余弦定理を使えば,答えが分かります。 \(a > 0\)に注意してください。
\( \begin{align} a^2 &= b^2 + c^2 - 2bc \cos A \\[5pt] &= (\sqrt{2})^2 + 5^2 - 2 \cdot \sqrt{2} \cdot 5 \displaystyle\frac{1}{\sqrt{2}} \\[5pt] &= 2 + 25 - 10 \\[5pt] &= 17 \\[5pt] \textcolor{red}{a} &\textcolor{red}{=} \textcolor{red}{\sqrt{17}} \end{align} \) -
問題の三角形の情報を適当な図にまとめます。
\(\angle \mathrm{C}\)の情報を活用できるように余弦定理を使えば,答えが分かります。 \(b > 0\)に注意してください。
\( \begin{align} c^2 &= a^2 + b^2 - 2ab \cos C \\[5pt] (\sqrt{19})^2 &= 2^2 + b^2 - 2 \cdot 2 \cdot b \cdot \left(-\displaystyle\frac{1}{2}\right) \\[5pt] 19 &= 4 + b^2 + 2b \\[5pt] b^2 + 2b - 15 &= 0 \\[5pt] (b - 3)(b + 5) &= 0 \\[5pt] \textcolor{red}{b} &\textcolor{red}{=} \textcolor{red}{3} \end{align} \) -
問題の三角形の情報を適当な図にまとめます。
\(\angle \mathrm{B}\)の情報を得られるように余弦定理を使えば,答えが分かります。
\( \begin{align} \cos B &= \displaystyle\frac{c^2 + a^2 - b^2}{2ca} \\[5pt] &= \displaystyle\frac{(\sqrt{2})^2 + 3^2 - (\sqrt{5})^2}{2 \cdot \sqrt{2} \cdot 3} \\[5pt] &= \displaystyle\frac{2 + 9 - 5}{6\sqrt{2}} \\[5pt] &= \displaystyle\frac{1}{\sqrt{2}} \\[5pt] \textcolor{red}{C} &\textcolor{red}{=} \textcolor{red}{45^{\circ}} \end{align} \) -
問題の三角形の情報を適当な図にまとめます。
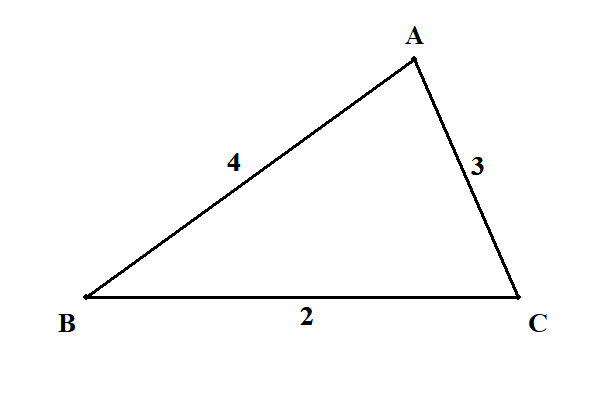
\(\angle \mathrm{C}\)の情報を得られるように余弦定理を使えば,答えが分かります。
\( \begin{align} \cos C &= \displaystyle\frac{a^2 + b^2 - c^2}{2ab} \\[5pt] &= \displaystyle\frac{2^2 + 3^2 - 4^2}{2 \cdot 2 \cdot 3} \\[5pt] &= \displaystyle\frac{4 + 9 - 16}{12} \\[5pt] \textcolor{red}{\cos C} &\textcolor{red}{=} \textcolor{red}{-\displaystyle\frac{1}{4}} \end{align} \)\(\cos C < 0\)なので,\(\angle \mathrm{C}\)は鈍角です。
本文で証明した余弦定理は,第2余弦定理といわれることもあります。 第2があるということは,第1もあるのですが,その内容は\(\triangle \mathrm{ABC}\)について,次の式が成り立つというものです。
1つめの式が成り立つことを証明してください。 \(\angle \mathrm{B}\)も\(\angle \mathrm{C}\)も鋭角の場合だけで良いです。
答え
\(\angle \mathrm{B}\)も\(\angle \mathrm{C}\)も鋭角の場合を考えれば良いので,次の図のような\(\triangle \mathrm{ABC}\)を考えれば良いです。
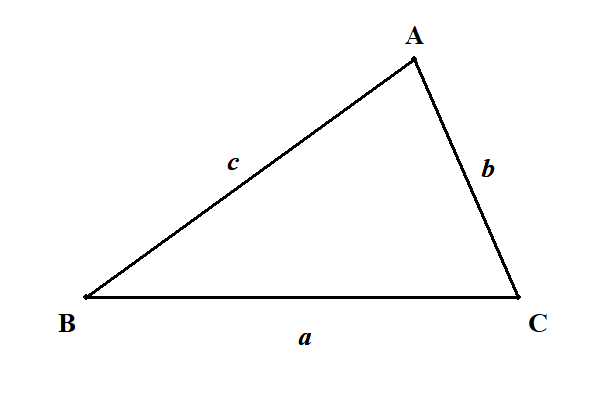
角\(\mathrm{A}\)から対辺に垂線\(\mathrm{AH}\)を下ろします。 直角三角形をつくるためです。
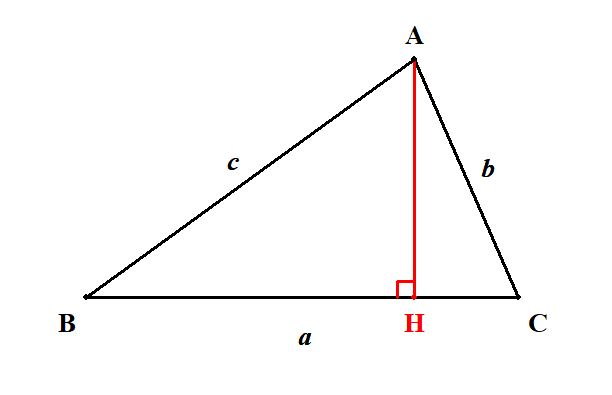
2つの直角三角形\(\triangle \mathrm{ABH}\)と\(\triangle \mathrm{ACH}\)ができています。 この情報を活用すれば,第1余弦定理を証明できます。
鈍角がある場合もほとんど同様に証明できます。
