前回,直角三角形を使って\(0^{\circ}\)~\(90^{\circ}\)の三角比を定義しました。 しかし,一般の三角形の角度には\(0^{\circ}\)~\(180^{\circ}\)がありえます。 どうやら三角比をより活用できるようにするためには,三角比を改良する必要がありそうです。
目次
三角比と単位円
三角比を拡張するとはいっても,直角三角形の角が\(90^{\circ}\)より大きい角度になることはありえません。 拡張のためには,定義の仕方自体を見直す必要がありそうです。
前回,直角三角形の辺の比として三角比を定義しました。 「比」って何だかややこしそうですが,斜辺の長さを\(1\)としてみてください。 ちょっとシンプルな感じになります。
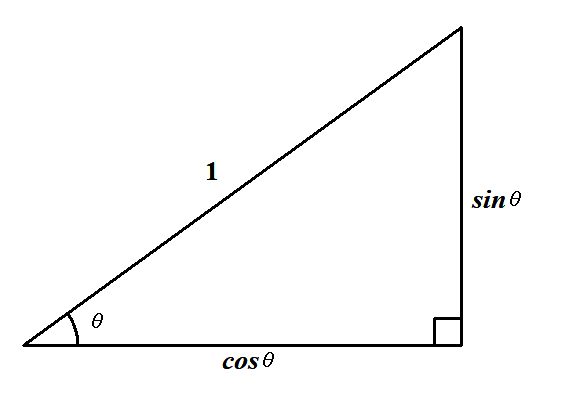
斜辺以外の辺がちょうど\(\sin\theta\),\(\cos\theta\)になりましたね。 \(\sin\theta\),\(\cos\theta\)は斜辺を分母とする比ですから,斜辺を\(1\)とすることで最もシンプルになるわけですね。
ここで\(\sin\theta\),\(\cos\theta\)は縦・横方向の長さですから,座標でうまく表せそうです。 下図のように座標軸を設定してみましょう。
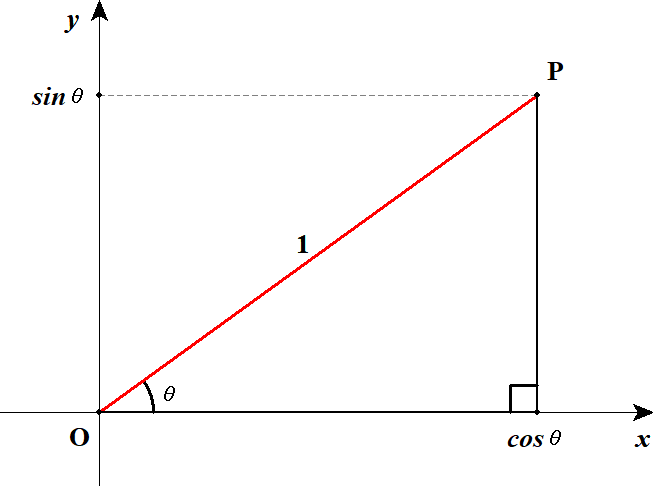
こうしてみると,三角比というのは,実は原点からの距離が\(1\)である点の座標であることが分かります。 それはつまり,原点を中心とする半径\(1\)の円周上の点の座標です。 下図を見てイメージしましょう。
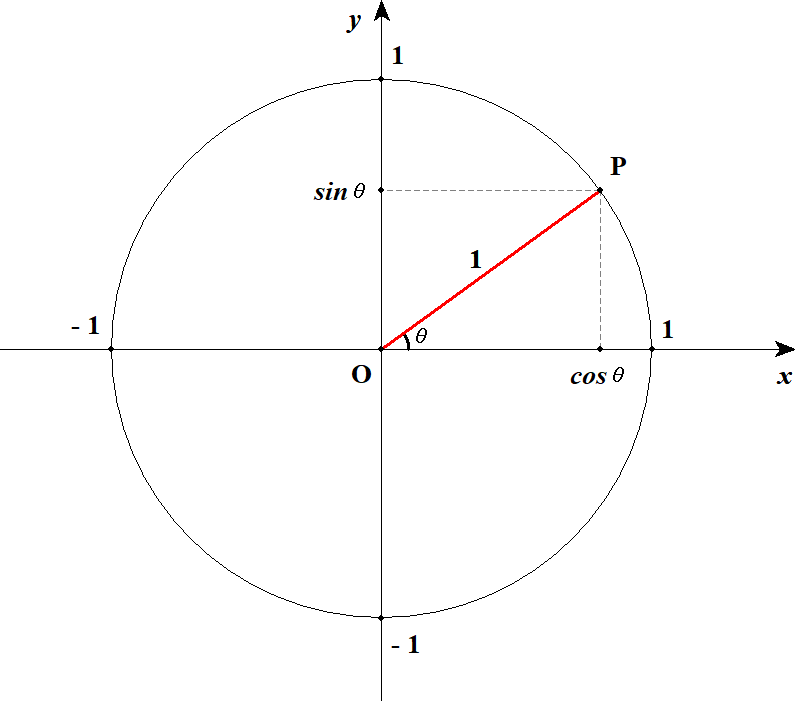
\(\theta\)の値を変えると図の赤い線がぐるぐる回ります。 そのときの点\(P\)の\(x\)座標が\(\cos\theta\),\(y\)座標が\(\sin\theta\)なんですね。 半径\(1\)の円のことを単位円といいますが,三角比は単位円によって定義できるわけです。
ところで,何か忘れてませんか? そう,\(\tan\theta\)の出番がまだきてないですね。 \(\tan\theta\)も単位円と結び付けてみましょう。 もういちど直角三角形の図を見てください。

\(\tan\theta\)がどこの比であったかを思い出すと,\(\tan\theta\)が次の式で表されることが分かります。
改めて先ほどの単位円の図を見てください。 この式は赤い線の傾きを表していることが分かりますか? \(x\)の増加量に対する\(y\)の増加量を表す比になっていますね。
\(\tan\theta\)が赤い線の傾きを表すことは分かりました。 これも図の中に表現してみましょう。
赤い線は原点を通り,傾きが\(\tan\theta\)ですから,その方程式は次のようになります。
この方程式を使って\(\tan\theta\)を図中に登場させるには,直線\(x = 1\)との交点をとれば良いです。 交点の\(y\)座標として\(\tan\theta\)が登場します。
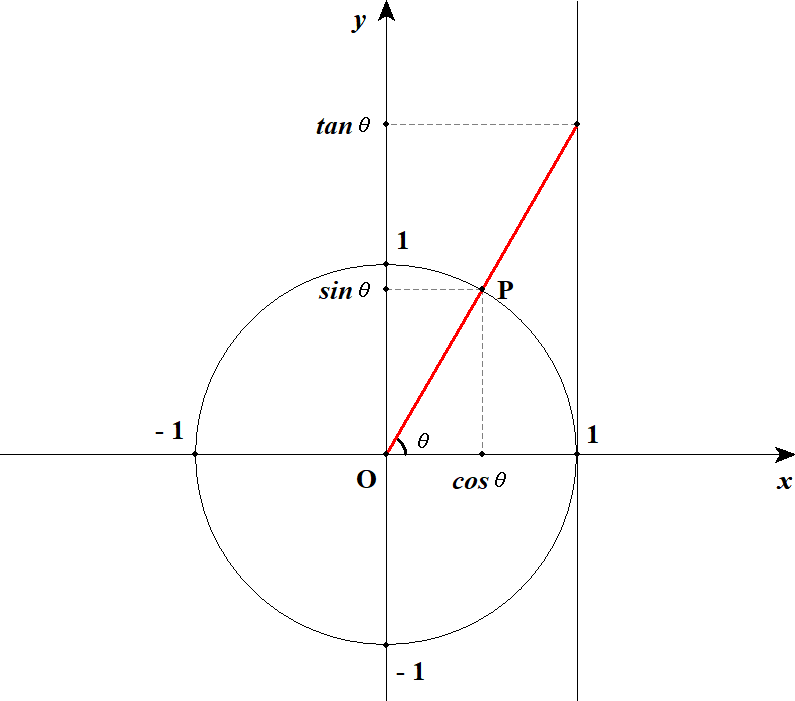
これで\(\tan\theta\)も含め,三角比を単位円\(+ \alpha\)を使って定義できました。 この定義を使って,三角比を拡張していきましょう。
三角比の拡張
それでは,三角比を拡張していきましょう。 前項で見た通り,三角比は単位円で定義できるわけですが,\(\theta\)をどんどん大きくしていくとどうなるでしょうか? 下図を見てください。
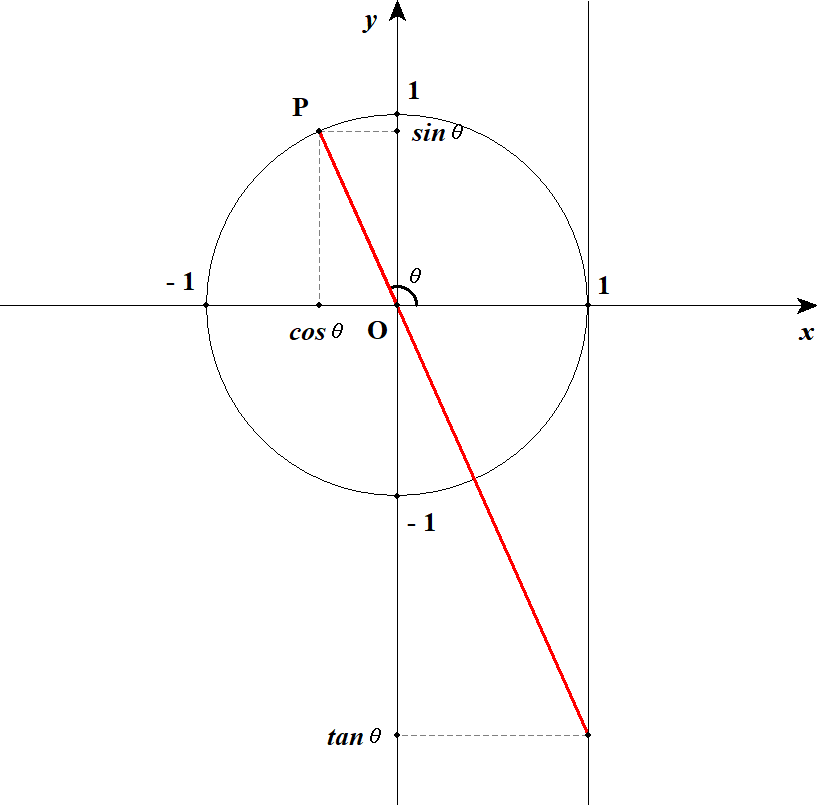
\(\theta\)が\(90^{\circ}\)を超えても三角比の定義がそのまま使えてますね。 しかも,点\(P\)が第2象限に移動したことから,三角比の符号が次のようになることが分かります。
■ 三角比の符号
| \(\theta\) | \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
|---|---|---|---|
| \(\theta = 0^{\circ}\) | \(0\) | \(+\) | \(0\) |
| \(0^{\circ} < \theta < 90^{\circ}\) | \(+\) | \(+\) | \(+\) |
| \(\theta = 90^{\circ}\) | \(+\) | \(0\) | 不可 |
| \(90^{\circ} < \theta < 180^{\circ}\) | \(+\) | \(-\) | \(-\) |
| \(\theta = 180^{\circ}\) | \(0\) | \(-\) | \(0\) |
\(\sin\theta\)は点\(P\)の\(y\)座標,\(\cos\theta\)は\(x\)座標,\(\tan\theta\)は赤線の傾きであることを考えれば,この符号の変化は簡単に理解できます。
また,\(\tan 90^{\circ}\)は定義できないことに注意してください。 \(\theta = 90^{\circ}\)のとき,赤い線は真上を向くことになり,傾きは考えられません。 (\(x\)の変化量が\(0\)なので,傾きの式の分母が\(0\)になってしまいます。)
数学Ⅰでは\(0^{\circ}\)~\(180^{\circ}\)の三角比しか考えませんが,もっと大きい\(\theta\)や負の\(\theta\)も考えられます。 詳しくは数学Ⅱで学びますが,単位円を使って同じように定義できるので,余裕があれば考えてみてください。
これで三角比の拡張が完了しましたが,じゃあ\(\cos 135^{\circ}\)の値は?と急に聞かれたら困ると思います。 次項で拡張した三角比の値について考えてみましょう。
余角と補角
拡張した三角比の値を計算できるようにしましょう。 拡張した定義は,直角三角形を使った定義を引き継いでいますから,\(0^{\circ}\)~\(90^{\circ}\)のときの値は前回学んだものと同じです。 このときの三角比の値は次のようになりますね。
| \(\theta\) | \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
|---|---|---|---|
| \(30^{\circ}\) | \(\displaystyle\frac{1}{2}\) | \(\displaystyle\frac{\sqrt{3}}{2}\) | \(\displaystyle\frac{1}{\sqrt{3}}\) |
| \(45^{\circ}\) | \(\displaystyle\frac{1}{\sqrt{2}}\) | \(\displaystyle\frac{1}{\sqrt{2}}\) | \(1\) |
| \(60^{\circ}\) | \(\displaystyle\frac{\sqrt{3}}{2}\) | \(\displaystyle\frac{1}{2}\) | \(\sqrt{3}\) |
この表を改めて見てみると,あることに気が付きます。 \(\sin 30^{\circ}\)と\(\cos 60^{\circ}\),\(\sin 60^{\circ}\)と\(\cos 30^{\circ}\)の値がそれぞれ同じですね。 このような角度の合計が\(90^{\circ}\)である2つの角を互いに余角であるといいます。 余角をとると\(\sin\)と\(\cos\)が入れ替わるんですね。
これは偶然ではなく,次の公式が成り立ちます。
- \(\sin(90^{\circ} - \theta) = \cos\theta\)
- \(\cos(90^{\circ} - \theta) = \sin\theta\)
- \(\tan(90^{\circ} - \theta) = \displaystyle\frac{1}{\tan\theta}\)
公式が成り立つことを確認しておきます。 下図のように,同じ直角三角形を向きを変えて2つ並べてみましょう。 直角でない角のうち,ひとつの角度を\(\theta\)とすると,もうひとつは\(90^{\circ} - \theta\)になります。
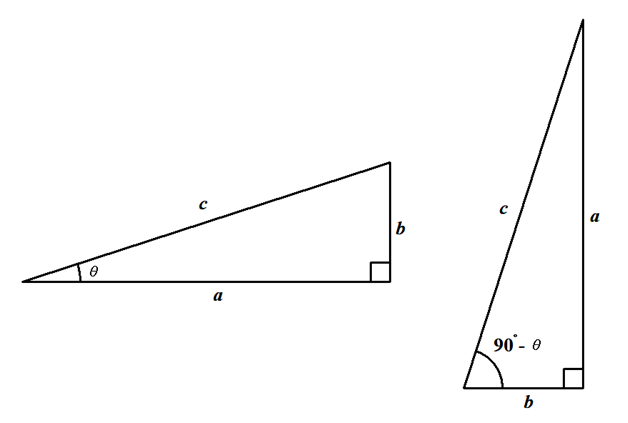
この図を使って\(\theta\)と\(90^{\circ} - \theta\)の三角比を比べると,\(\sin\)と\(\cos\)が入れ替わることが確認できます。 同じ三角形の向きを変えたことで,比をとる辺が入れ替わったからですね。 同様に\(\tan\)についても,比の分母分子が入れ替わることが分かります。
\(0^{\circ} < \theta < 90^{\circ}\)の三角比についてはよく分かりました。 その他の\(\theta\)についても考えましょう。 まずは\(90^{\circ} < \theta < 180^{\circ}\)を考えます。
例として\(\cos 135^{\circ}\)の値を考えます。 下図の状況を考えれば良いですね。
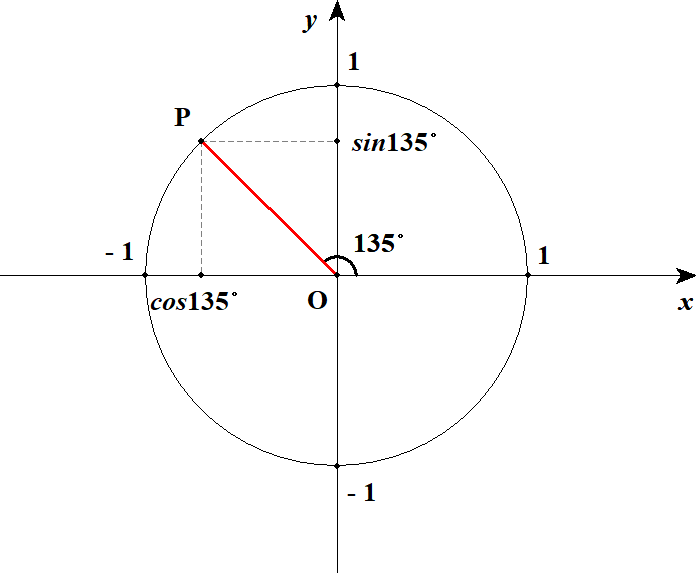
図を見ると気づくことがあります。 今までは第1象限に赤線を斜辺とする直角三角形ができていましたが,今回は第2象限に直角三角形ができています。 この直角三角形に注目すると,下図のように\(45^{\circ}\)の三角比を使って考えられるようになります。
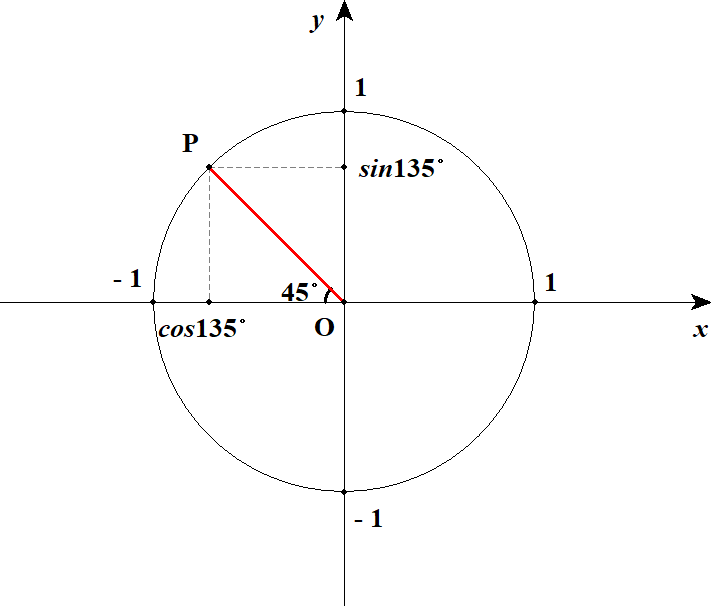
こうして見れば\(\cos 135^{\circ}\)の値はすぐ分かりますね。 \(y\)軸をはさんで,ちょうど\(\cos 45^{\circ}\)の反対側にあるので,次の値になります。
ついでに\(\sin 135^{\circ}\)についても考えてみると,図から\(\sin 45^{\circ}\)と全く同じ値になることが分かります。 \(\tan 135^{\circ}\)については,赤線を右側に延長した図を想像すると,\(x\)軸をはさんで,ちょうど\(\tan 45^{\circ}\)の反対側にあることが分かります。
\(45^{\circ}\)と\(135^{\circ}\)のように,角度の合計が\(180^{\circ}\)である2つの角を互いに補角であるといいます。 上で考えたように,補角について次の公式が成り立ちます。
- \(\sin(180^{\circ} - \theta) = \sin\theta\)
- \(\cos(180^{\circ} - \theta) = -\cos\theta\)
- \(\tan(180^{\circ} - \theta) = -\tan\theta\)
補角を考えるとき,図の赤線がちょうど\(y\)軸をはさんで反対側に移ります。 その図を思い浮かべれば,\(\sin\)は変わらないし,\(\cos\)は符号が反転するし,\(\tan\)も符号が反転することが分かります。
あと確認できていない\(\theta\)は,ちょうど\(0^{\circ}\),\(90^{\circ}\),\(180^{\circ}\)の場合ですね。 これは単位円をかけば簡単に分かるので,確認問題にしておきます。
確認問題
\(\theta\)が\(0^{\circ}\),\(90^{\circ}\),\(180^{\circ}\)の場合の三角比を考えたいと思います。 それぞれの場合の三角比の値を求め,次の表を埋めてください。
| \(\theta\) | \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
|---|---|---|---|
| \(0^{\circ}\) | |||
| \(90^{\circ}\) | 不可 | ||
| \(180^{\circ}\) |
答え
単位円を思い浮かべれば簡単です。 単位円の図の赤線は\(\theta = 0^{\circ}\)のときは右に倒れた状態です。 \(\theta = 90^{\circ}\)のときは直立,\(\theta = 180^{\circ}\)のときは左に倒れた状態です。 したがって,三角比の値は次のようになります。
| \(\theta\) | \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
|---|---|---|---|
| \(0^{\circ}\) | \(0\) | \(1\) | \(0\) |
| \(90^{\circ}\) | \(1\) | \(0\) | 不可 |
| \(180^{\circ}\) | \(0\) | \(-1\) | \(0\) |
余角の公式と補角の公式を使って,次の式を証明してください。
-
\(\sin(90^{\circ} + \theta) = \cos\theta\)
-
\(\cos(90^{\circ} + \theta) = -\sin\theta\)
-
\(\tan(90^{\circ} + \theta) = -\displaystyle\frac{1}{\tan\theta}\)
答え
余角・補角の公式を使えるように工夫します。 余角の公式は\(90^{\circ} - \theta\),補角の公式は\(180^{\circ} - \theta\)を使う公式です。 これを活用して\(90^{\circ} + \theta\)をつくるには,\(90 = 180 - 90\)であることに注目すれば良いです。
-
次の計算で証明できます。 補角の公式・余角の公式の順で使います。
\( \begin{align} \sin(90^{\circ} + \theta) &= \sin\{180^{\circ} - (90^{\circ} - \theta)\} \\[5pt] &= \sin(90^{\circ} - \theta) \\[5pt] &= \cos\theta \end{align} \) -
次の計算で証明できます。 補角の公式・余角の公式の順で使います。
\( \begin{align} \cos(90^{\circ} + \theta) &= \cos\{180^{\circ} - (90^{\circ} - \theta)\} \\[5pt] &= -\cos(90^{\circ} - \theta) \\[5pt] &= -\sin\theta \end{align} \) -
次の計算で証明できます。 補角の公式・余角の公式の順で使います。
\( \begin{align} \tan(90^{\circ} + \theta) &= \tan\{180^{\circ} - (90^{\circ} - \theta)\} \\[5pt] &= -\tan(90^{\circ} - \theta) \\[5pt] &= -\displaystyle\frac{1}{\tan\theta} \end{align} \)
次の値を求めてください。
-
\(\sin 150^{\circ}\)
-
\(\cos 120^{\circ}\)
-
\(\tan 135^{\circ}\)
-
\(\sin 135^{\circ}\)
-
\(\cos 150^{\circ}\)
-
\(\tan 120^{\circ}\)
答え
補角の公式を活用しましょう。 補角の公式を暗記する必要はありません。 単位円を思い浮かべれば,符号が変化するかどうか簡単に分かります。
-
\(\sin 150^{\circ} = \sin 30^{\circ} = \textcolor{red}{\displaystyle\frac{1}{2}}\)
-
\(\cos 120^{\circ} = -\cos 60^{\circ} = \textcolor{red}{-\displaystyle\frac{1}{2}}\)
-
\(\tan 135^{\circ} = -\tan 45^{\circ} = \textcolor{red}{-1}\)
-
\(\sin 135^{\circ} = \sin 45^{\circ} = \textcolor{red}{\displaystyle\frac{1}{\sqrt{2}}}\)
-
\(\cos 150^{\circ} = -\cos 30^{\circ} = \textcolor{red}{-\displaystyle\frac{\sqrt{3}}{2}}\)
-
\(\tan 120^{\circ} = -\tan 60^{\circ} = \textcolor{red}{-\sqrt{3}}\)
\(\sin 25^{\circ} = a\),\(\cos 40^{\circ} = b\)としたとき,次の式を\(a, b\)で表してください。
答え
与えられた三角比の値は,角度が\(25^{\circ}\),\(40^{\circ}\)のものです。 しかし問題の式に登場するのは,もっと大きな角度の三角比です。
与えられた値を使うため,\(90^{\circ}\)以上の三角比には補角の公式,\(45^{\circ}\)以上の三角比には余角の公式を使うことで,小さな角度の三角比にもっていきましょう。
式に登場するパーツをひとつひとつ変形しておきます。
以上より,問題の式が次のように計算できます。
ある関数\(f(x)\)について,定義域内で\(x\)が増加するにつれて\(f(x)\)も常に増加するとき,\(f(x)\)は単調増加するといいます。 逆に\(f(x)\)が常に減少する場合は,単調減少するといいます。
三角比\(\sin\theta\),\(\cos\theta\),\(\tan\theta\)を\(\theta\)の関数として考えて,単調増加または単調減少するか考えてみましょう。
\(\theta\)の定義域を鋭角(\(0^{\circ} < \theta < 90^{\circ}\)),または鈍角(\(90^{\circ} < \theta < 180^{\circ}\))に限定して考えたとき,各三角比が単調増加するか,単調減少するか,どちらでもないか答えてください。
解答は次の表に,単調増加するなら\(+\),単調減少するなら\(-\),どちらでもないなら\(\pm\)と入れてください。
| 定義域 | \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
|---|---|---|---|
| 鋭角 | |||
| 鈍角 |
答え
単位円の定義に慣れるための練習になる問題です。 それぞれの三角比の定義を思い出しながら考えましょう。
まず\(\sin\theta\)についてですが,これは単位円周上の\(y\)座標でしたね。 \(\theta\)が鋭角の間は\(y\)座標が増加していきますが,円の頂上にたどりつくと,\(\theta\)は鈍角になり,今度は円を下って減少していきます。
次に\(\cos\theta\)についてですが,これは単位円周上の\(x\)座標でしたね。 \(\theta\)が鋭角でも鈍角でも,円周上の点はどんどん左の方に向かっていくので,\(\cos\theta\)はずっと単調減少です。
ちょっとややこしいのが\(\tan\theta\)です。 \(\tan\theta\)は原点と単位円周上の点を結ぶ線分を延長し,直線\(x = 1\)とぶつかる点の\(y\)座標でしたね。 \(\theta\)が鋭角の間は,交点の\(y\)座標が増加していきます。 しかも値の増え方は急激で,\(90^{\circ}\)近くなると交点は遥か上方にあります。
\(\theta\)がちょうど\(90^{\circ}\)になると,原点と円周上の点を結ぶ直線は,直線\(x = 1\)と平行になってしまうので,交点がありません。 なので\(\tan90^{\circ}\)は定義されていません。
\(\theta\)が\(90^{\circ}\)を超え鈍角になると,今度は交点が遥か下方から現れます。 そして\(\tan\theta\)は急激に増加していきます。 したがって,\(\tan\theta\)は鋭角でも鈍角でも単調増加です。
\(\tan\theta\)はずっと増加し続けているのに,鋭角では正の値,鈍角では負の値をとります。 すこし不思議な感じがしますが,これは\(\theta\)が\(90^{\circ}\)を超えるときに,\(\tan\theta\)が限りなく大きい値から,急に限りなく小さい値に飛ぶからですね。
以上から,解答は次のようになります。
| 定義域 | \(\sin\theta\) | \(\cos\theta\) | \(\tan\theta\) |
|---|---|---|---|
| 鋭角 | \(+\) | \(-\) | \(+\) |
| 鈍角 | \(-\) | \(-\) | \(+\) |
