三角形の外心・内心・重心を考えます。 これらは円との関係が深かったり,物理的に重要な意味を持っています。 また,共点を考えるよい練習にもなります。
目次
二等分線の性質
外心などについて話をする前に,準備として線分の垂直二等分線と角の二等分線について考えます。
まずは線分の垂直二等分線について,次が成り立つことを確認しておきましょう。
線分\(\mathrm{AB}\)の垂直二等分線上の点は,\(2\)点\(\mathrm{A}\),\(\mathrm{B}\)からの距離が等しい。
逆に\(2\)点\(\mathrm{A}\),\(\mathrm{B}\)からの距離が等しい点は,線分\(\mathrm{AB}\)の垂直二等分線上にある。
これを証明します。 線分\(\mathrm{AB}\)の中点を\(\mathrm{M}\)とすると,この点は\(2\)点\(\mathrm{A}\),\(\mathrm{B}\)からの距離が等しいです。 垂直二等分線上に\(\mathrm{M}\)以外の好きな点\(\mathrm{P}\)をとり,これも\(2\)点\(\mathrm{A}\),\(\mathrm{B}\)からの距離が等しいことを示します。
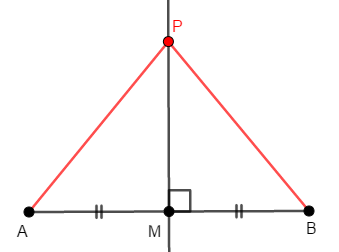
このとき,\(\triangle\mathrm{PMA}\)と\(\triangle\mathrm{PMB}\)について,\(\mathrm{AM} = \mathrm{BM}\),\(\angle\mathrm{PMA} = \angle\mathrm{PMB}\)が成り立ち,\(\mathrm{PM}\)が共通です。 \(2\)辺とその間の角がそれぞれ等しいですから,\(\triangle\mathrm{PMA}\)と\(\triangle\mathrm{PMB}\)は合同であり,対応する辺が等しいので,\(\mathrm{PA} = \mathrm{PB}\)となります。
これで点\(\mathrm{P}\)も,\(2\)点\(\mathrm{A}\),\(\mathrm{B}\)からの距離が等しいことが分かりました。
逆についても考えます。 線分\(\mathrm{AB}\)の中点を\(\mathrm{M}\)とすると,この点は線分\(\mathrm{AB}\)の垂直二等分線上にあります。 \(2\)点\(\mathrm{A}\),\(\mathrm{B}\)からの距離が等しい\(\mathrm{M}\)以外の好きな点\(\mathrm{P}\)をとり,この点も線分\(\mathrm{AB}\)の垂直二等分線上にあることを示します。
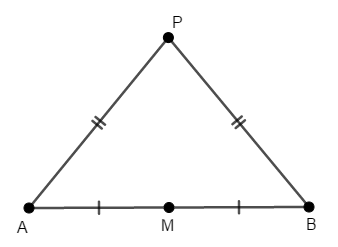
ここで\(\triangle\mathrm{PAB}\)は二等辺三角形ですから,頂角\(\mathrm{APB}\)の二等分線は底辺を垂直に二等分します。
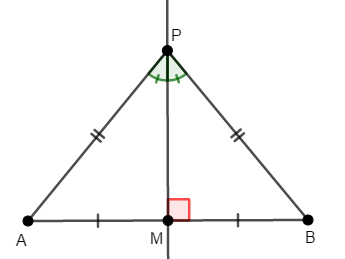
これで点\(\mathrm{P}\)も,線分\(\mathrm{AB}\)の垂直二等分線上にあることが分かりました。
次に角の二等分線について,次が成り立つことを確認しておきましょう。
\(\angle\mathrm{AXB}\)の二等分線上の点は,\(2\)直線\(\mathrm{XA}\),\(\mathrm{XB}\)からの距離が等しい。
逆に\(2\)直線\(\mathrm{XA}\),\(\mathrm{XB}\)からの距離が等しい点は,\(\angle\mathrm{AXB}\)の二等分線上にある。
点と直線の距離というのは,点から直線に引いた垂線の長さのことです。
一般に\(2\)つの図形の距離というのは,それぞれの図形の点のうち最も近い位置にある点同士の距離のことです。 点と直線上の点が最も近くなるのは,それらを結ぶ線分が垂線になるときですね。
これを証明します。 点\(\mathrm{X}\)自身はどちらの直線とも距離が\(0\)ですね。 \(\angle\mathrm{AXB}\)の二等分線上の\(\mathrm{X}\)以外の好きな点\(\mathrm{P}\)をとり,この点も\(2\)直線\(\mathrm{XA}\),\(\mathrm{XB}\)からの距離が等しいことを示します。
点\(\mathrm{P}\)から直線\(\mathrm{XA}\),\(\mathrm{XB}\)にそれぞれ垂線を下ろします。 その交点をそれぞれ\(\mathrm{H}_1\),\(\mathrm{H}_2\)とします。
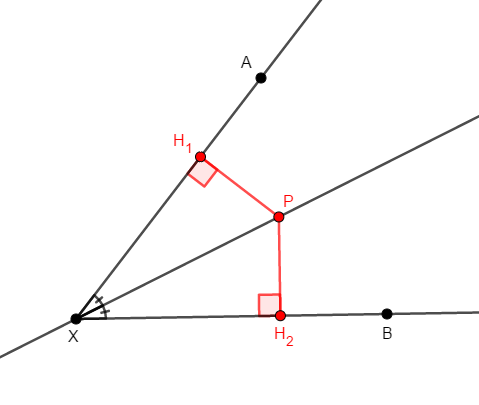
直角三角形\(\triangle\mathrm{PXH}_1\),\(\triangle\mathrm{PXH}_2\)に注目すると,斜辺\(\mathrm{PX}\)が共通であり,\(\angle\mathrm{PXH}_1 = \angle\mathrm{PXH}_2\)が成り立ちます。 直角三角形の斜辺と\(1\)つの鋭角がそれぞれ等しいですから,\(\triangle\mathrm{PXH}_1\)と\(\triangle\mathrm{PXH}_2\)は合同であり,対応する辺が等しいので,\(\mathrm{PH}_1 = \mathrm{PH}_2\)となります。
これで点\(\mathrm{P}\)も,\(2\)直線\(\mathrm{XA}\),\(\mathrm{XB}\)からの距離が等しいことが分かりました。
逆についても考えます。 点\(\mathrm{X}\)自身は,\(\angle\mathrm{AXB}\)の二等分線上にあります。 \(2\)直線\(\mathrm{XA}\),\(\mathrm{XB}\)からの距離が等しい\(\mathrm{X}\)以外の好きな点\(\mathrm{P}\)をとり,この点も\(\angle\mathrm{AXB}\)の二等分線上にあることを示します。
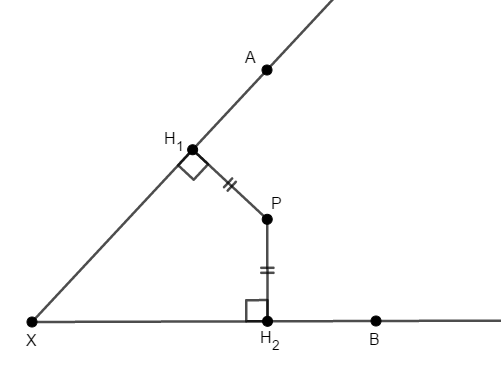
直線\(\mathrm{XA}\),\(\mathrm{XB}\)が点\(\mathrm{P}\)から下ろした垂線と交わる点をそれぞれ\(\mathrm{H}_1\),\(\mathrm{H}_2\)としています。
ここで直角三角形\(\triangle\mathrm{PXH}_1\),\(\triangle\mathrm{PXH}_2\)に注目すると,斜辺\(\mathrm{PX}\)が共通であり,\(\mathrm{PH}_1 = \mathrm{PH}_2\)が成り立ちます。 直角三角形の斜辺と他の\(1\)辺がそれぞれ等しいですから,\(\triangle\mathrm{PXH}_1\)と\(\triangle\mathrm{PXH}_2\)は合同であり,対応する角が等しいので,\(\angle\mathrm{PXH}_1 = \angle\mathrm{PXH}_2\)となります。
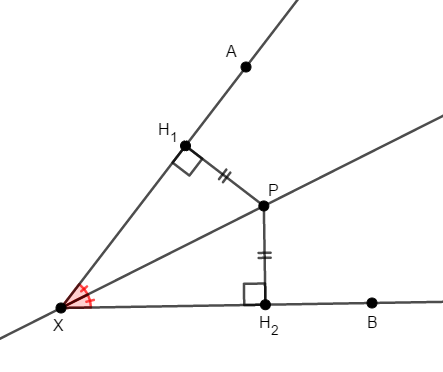
これで点\(\mathrm{P}\)も,\(\angle\mathrm{AXB}\)の二等分線上にあることが分かりました。
外心
準備が整ったところで,まず外心について学びましょう。 先に結論を書いておきます。 それから詳しい議論をしていきましょう。
三角形の各辺の垂直二等分線は\(1\)点で交わる。 また,この共有点はこの三角形の外心である。
三角形の\(3\)頂点を通る円のことを,その三角形の外接円といいます。 三角形に外側から接するような円ですね。
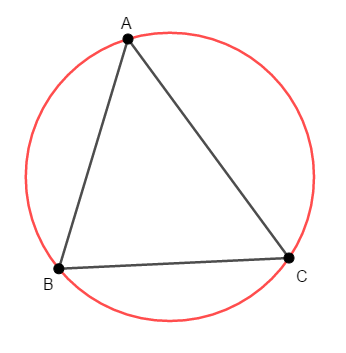
外接円の中心を外心といいますが,三角形の外心はどこにあるのでしょうか? その答えが先ほどの定理で,\(3\)辺の垂直二等分線の交点が外心になります。 その理由を考えてみましょう。
円の半径はどこでも一定ですから,外心と三角形の各頂点を結ぶ線分はすべて同じ長さです。
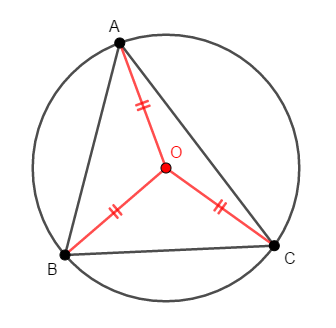
ということは,外心は各頂点からの距離が等しい点です。 前項で確認した通り,\(2\)頂点からの距離が等しい点は,それらを結ぶ辺の垂直二等分線上にあります。 だからどの頂点からの距離も等しい点は,\(3\)辺の垂直二等分線の交点だということになるのです。
しかもそのような点は,どんな三角形に対しても必ずあります。 つまり三角形には必ず外接円が存在します。 (四角形にも同様に外接円が考えられますが,四角形の外接円は必ずしも存在しません。)
三角形の外接円が必ず存在することを証明するには,\(3\)辺の垂直二等分線は共点であることを示せば良いです。 さっそくやってみましょう。
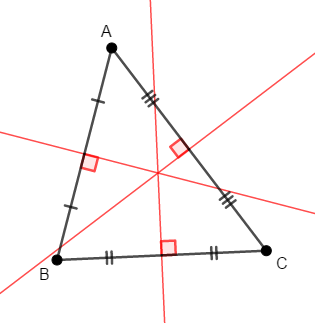
といっても,これは難しい話ではありません。 共点を示す方針はいくつかありますが,\(2\)直線の交点が,残りの直線上の点でもあることを証明します。
辺\(\mathrm{AB}\)の垂直二等分線上の点は,頂点\(\mathrm{A}\),\(\mathrm{B}\)からの距離が等しいです。 辺\(\mathrm{BC}\)の垂直二等分線上の点についても,同様のことがいえますから,それらの交点を\(\mathrm{P}\)とすると,次が成り立ちます。
点\(\mathrm{P}\)はどちらの垂直二等分線上の点でもあるので,このように両者の性質を併せ持つわけですね。
これらの式を組み合わせると\(\mathrm{PC} = \mathrm{PA}\)が成り立ちますから,点\(\mathrm{P}\)は\(2\)頂点\(\mathrm{C}\),\(\mathrm{A}\)からの距離が等しい点でもあります。 したがって,点\(\mathrm{P}\)は辺\(\mathrm{CA}\)の垂直二等分線上の点でもあるので,\(3\)辺の垂直二等分線は共点です。
これで三角形には必ず外接円が存在し,外心は各辺の垂直二等分線の交点であることが分かりましたね。
内心
次は内心について学びますが,やはり先に結論を書いておきます。 それから詳しい議論をしていきましょう。
三角形の各内角の二等分線は\(1\)点で交わる。 また,この共有点はこの三角形の内心である。
三角形の\(3\)辺に接する円のことを,その三角形の内接円といいます。 三角形に内側から接するような円ですね。
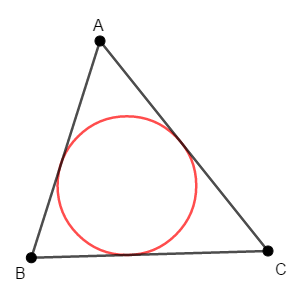
内接円の中心を内心といいますが,三角形の内心はどこにあるのでしょうか? その答えが先ほどの定理で,\(3\)内角の二等分線の交点が内心になります。 その理由を考えてみましょう。
内接円は三角形の各辺と接していますから,その接点と内心を結ぶ線分は,各辺の垂線になります。 また,その垂線は円の半径ですから,すべて同じ長さです。
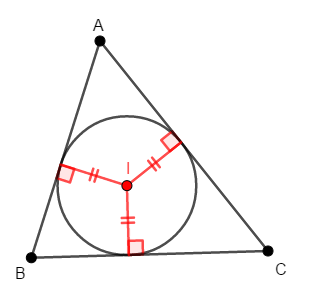
ということは,内心は各辺からの距離が等しい点です。 今回初めの項で確認した通り,\(2\)辺からの距離が等しい点は,その間の内角の二等分線上にあります。 だからどの辺からの距離も等しい点は,\(3\)内角の二等分線の交点だということになるのです。
しかもそのような点は,どんな三角形に対しても必ずあります。 つまり三角形には必ず内接円が存在します。 (外接円の場合と同じく,四角形の内接円は必ずしも存在しません。)
三角形の内接円が必ず存在することを証明するには,\(3\)内角の二等分線が共点であることを示せば良いです。 さっそくやってみましょう。
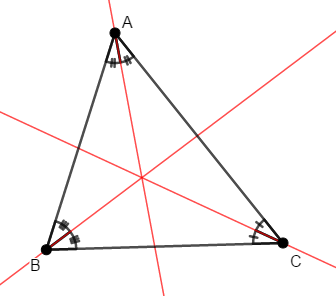
といっても,これは難しい話ではありません。 共点を示す方針はいくつかありますが,\(2\)直線の交点が,残りの直線上の点でもあることを証明します。
\(\angle\mathrm{A}\)の二等分線と\(\angle\mathrm{B}\)の二等分線の交点を\(\mathrm{P}\)とします。 また,そこから辺\(\mathrm{BC}\),\(\mathrm{CA}\),\(\mathrm{AB}\)に下ろした垂線をそれぞれ\(\mathrm{PH}_1\),\(\mathrm{PH}_2\),\(\mathrm{PH}_3\)としましょう。
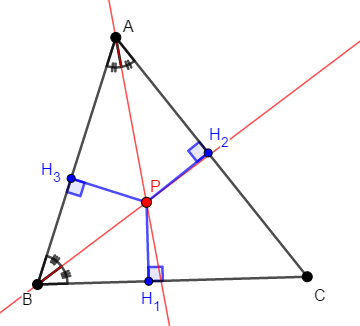
\(\angle\mathrm{A}\)の二等分線上の点は,辺\(\mathrm{AB}\),\(\mathrm{AC}\)からの距離が等しいです。 \(\angle\mathrm{B}\)の二等分線上の点についても,同様のことがいえますから,次が成り立ちます。
点\(\mathrm{P}\)はどちらの二等分線上の点でもあるので,このように両者の性質を併せ持つわけですね。
これらの式を組み合わせると\(\mathrm{PH}_1 = \mathrm{PH}_2\)が成り立ちますから,点\(\mathrm{P}\)は\(2\)辺\(\mathrm{CA}\),\(\mathrm{CB}\)からの距離が等しい点でもあります。 したがって,点\(\mathrm{P}\)は\(\angle\mathrm{C}\)の二等分線上の点でもあるので,\(3\)内角の二等分線は共点です。
これで三角形には必ず内接円が存在し,内心は各内角の二等分線の交点であることが分かりましたね。
重心
今回はもうひとつ重心を学んで終わりとします。 まずは結論から。
三角形の各中線は\(1\)点で交わる。 この共有点をこの三角形の重心と呼ぶ。
また,重心は各中線を頂点の側から\(2 : 1\)に内分する。
忘れた方もいるかもしれませんが,中線とは,三角形の頂点とその対辺の中点を結ぶ線分です。 中線定理なんてものもありましたね。
外心・内心と違い,重心は円とは関係ありません。 重心は「重さ」の中心なのです。 重さの偏りがない三角形の板を\(1\)本の針だけで支えるとき,針を重心に合わせれば良いです。
では三角形の重心はどこにあるのでしょうか? その答えが先ほどの定理で,\(3\)中線の交点が重心になります。 その理由を考えてみましょう。
ざっくり考えると,重心は三角形の「真ん中」にあるはずです。 ですから,重心は中線上のどこかにありそうだと思います。
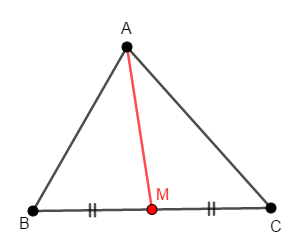
上図は頂点\(\mathrm{A}\)から引いた中線ですが,同様に他の頂点からも中線を引くと,その交点はあらゆる角度から「真ん中」だといえそうです。 実際,その交点が重心だというのが定理の内容です。
しかし,これは直感の話しかしておらず,数学的な議論ではありません。 直感が正しいことを証明する必要がありますね。 そのために次の\(2\)点を確認する必要があります。
- \(3\)本の中線は本当に共点か?
- 中線の交点は本当に重心か?
後者をきちんと議論しようとすると,物理学の知識が必要になるので,ここではとりあえず触れないことにします。 (直感的にそれっぽい!と感じられる問題を確認問題に載せておきます。) 数学での三角形の重心は,あくまで中線の交点として定義されます。
というわけで中線の共点問題を考えましょう。 ここでは「\(2\)直線ずつの交点が一致することを示す」方針でいきます。
辺\(\mathrm{BC}\),\(\mathrm{CA}\),\(\mathrm{AB}\)の中点をそれぞれ\(\mathrm{L}\),\(\mathrm{M}\),\(\mathrm{N}\)としましょう。 まず,中線\(\mathrm{AL}\)と\(\mathrm{BM}\)の交点\(\mathrm{G}_1\)を考えます。
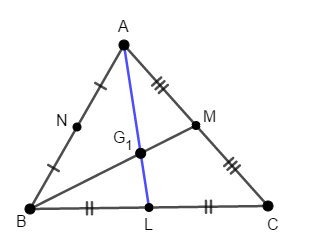
点\(\mathrm{G}_1\)が線分\(\mathrm{AL}\)をどんな比で内分するかを考えます。 辺の中点をたくさんとっていますから,中点連結定理を利用します。 次のように補助線\(\mathrm{LM}\)を引くと,中点連結定理により\(\mathrm{AB} /\!/ \mathrm{LM}\)です。
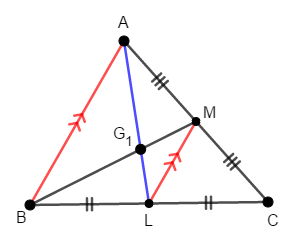
同じく中点連結定理により,\(\mathrm{AB} : \mathrm{LM} = 2 : 1\)であることも分かります。 したがって平行線と線分の比により,次が成り立ちます。
平行線と線分の比を覚えていない人は,三角形の相似を考えましょう! 等しい錯角を考えれば,\(\triangle\mathrm{ABG}_1\)と\(\triangle\mathrm{LMG}_1\)が相似であることが分かり,上の式が得られます。
次に,中線\(\mathrm{AL}\)と\(\mathrm{CN}\)の交点\(\mathrm{G}_2\)を考えます。
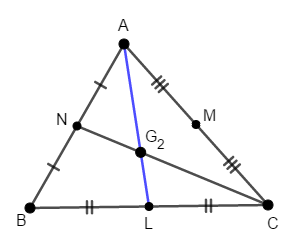
先ほどと同様に点\(\mathrm{G}_2\)が線分\(\mathrm{AL}\)をどんな比で内分するかを考えます。 もしこの比が,\(\mathrm{G}_1\)が線分\(\mathrm{AL}\)を内分する比と同じであれば,\(\mathrm{G}_1\)と\(\mathrm{G}_2\)は一致します。 同じ線分を同じ比で内分する点は,当然完全に同じ位置にある点ですよね。
先ほどと同じく中点連結定理を利用します。 次のように補助線\(\mathrm{NL}\)を引くと,中点連結定理により\(\mathrm{CA} /\!/ \mathrm{NL}\)です。
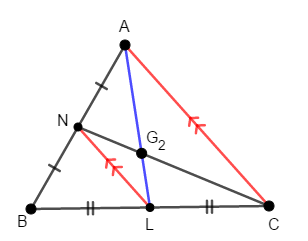
同じく中点連結定理により,\(\mathrm{CA} : \mathrm{NL} = 2 : 1\)であることも分かります。 したがって平行線と線分の比により,次が成り立ちます。
これで\(\mathrm{AG}_1 : \mathrm{G}_1\mathrm{L} = \mathrm{AG}_2 : \mathrm{G}_2\mathrm{L}\)であり,\(\mathrm{G}_1\)と\(\mathrm{G}_2\)が一致することが分かりました。 つまり\(3\)本の中線は共点だということですね。
全く同様の議論で\(\mathrm{BG} : \mathrm{GM} = 2 : 1\)と\(\mathrm{CG} : \mathrm{GN} = 2 : 1\)も分かります。 これで重心が中線を内分する比も分かりましたね。
重心が中線を内分する比が\(2 : 1\)か\(1 : 2\)か迷うことがあるかもしれません。 しかしこれは,重心が重さの中心であることを考慮すれば,簡単に分かります。
例えば先ほどの図で中線\(\mathrm{AL}\)を考えます。 明らかに\(\mathrm{A}\)側よりも\(\mathrm{L}\)側の方が重いですよね。
だから重さの中心,つまり重心\(\mathrm{G}\)は当然\(\mathrm{L}\)に近い方にあります。 だから\(\mathrm{AG} : \mathrm{GL} = 2 : 1\)だと思い出せます。 \(1 : 2\)ではありません。
確認問題
次の図で,\(\mathrm{O}\)は\(\triangle\mathrm{ABC}\)の外心です。 \(\angle\mathrm{BAC}\)を求めてください。
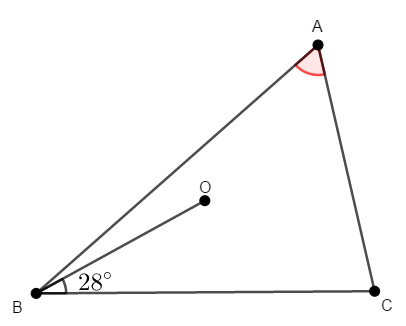
答え
外心は外接円の中心ですから,角度の計算には円周角の定理など,円の性質を利用できます。 考えやすいように外接円をかいておきましょう。
\(\mathrm{OB}\)や\(\mathrm{OC}\)は外接円の半径なので,同じ長さですね。
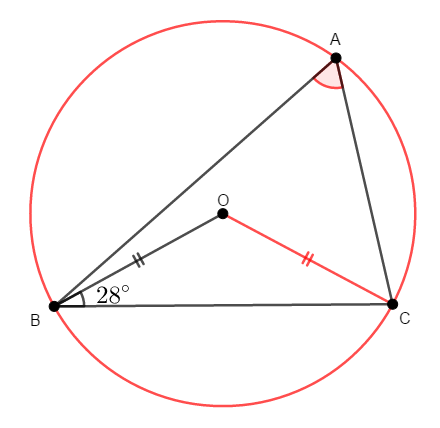
\(\triangle\mathrm{OBC}\)は二等辺三角形ですから,底角が等しいです。 したがって,\(\angle\mathrm{BOC}\)が次のように求められます。
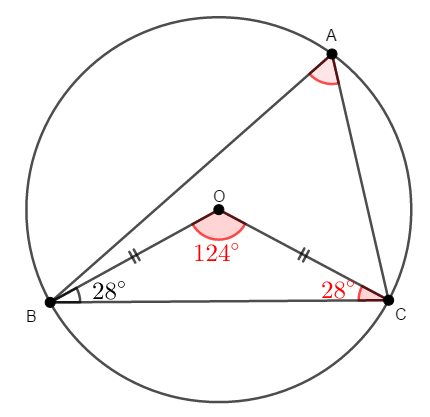
ここで\(\angle\mathrm{BOC}\)は中心角,\(\angle\mathrm{BAC}\)はそれと同じ弧に対する円周角ですから,円周角の定理により,\(\angle\mathrm{BAC}\)が次のように求められます。
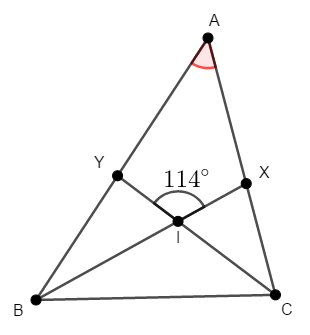
次の図で,\(\mathrm{I}\)は\(\triangle\mathrm{ABC}\)の内心です。 \(\angle\mathrm{BAC}\)を求めてください。
答え
内心は内接円の中心ですが,円の性質はあまり利用できなさそうです。 内接円は三角形の辺に接しているだけで,使えそうな円周角などが見つかりません。
内心は三角形の各内角の二等分線の交点ですから,内角が二等分されていることに注目しましょう。 \(\angle\mathrm{ABI} = \angle\mathrm{CBI}\),\(\angle\mathrm{ACI} = \angle\mathrm{BCI}\)ですね。
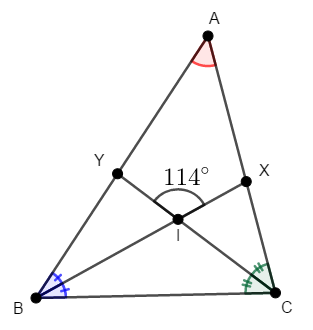
対頂角は等しいので\(\angle\mathrm{BIC} = \angle\mathrm{YIX}\)ですから,青い角と緑の角の和が分かります。
\(\angle\mathrm{ABC}\)は青い角\(2\)個分,\(\angle\mathrm{ACB}\)は緑の角\(2\)個分ですから,\(\angle\mathrm{BAC}\)が求められます。
\(\triangle\mathrm{ABC}\)の重心を\(\mathrm{G}\)とするとき,\(3\)つの三角形\(\triangle\mathrm{GAB}\),\(\triangle\mathrm{GBC}\),\(\triangle\mathrm{GCA}\)の面積が等しいことを証明してください。
(重心が重さの中心であることを何となく実感できますね。)
答え
重心は三角形を\(3\)等分や\(6\)等分する際にも役立ちます。 \(6\)等分の話を挟むため,次の解答例は少し遠回りしてあります。 解答の後に,もっとストレートな証明も補足しておきます。
イメージしやすいように,まずは簡単な図をかいておきましょう。 \(\triangle\mathrm{ABC}\)の面積を\(S\)としておきます。
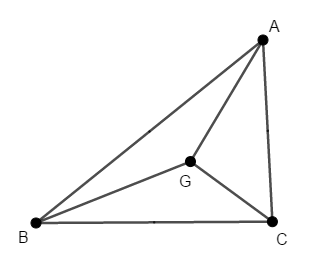
重心に関する情報をフル活用するために,線分\(\mathrm{AG}\)を辺\(\mathrm{BC}\)上まで延長し,点\(\mathrm{M}\)をとります。 重心の定義より,\(\mathrm{M}\)は辺\(\mathrm{BC}\)の中点ですね。
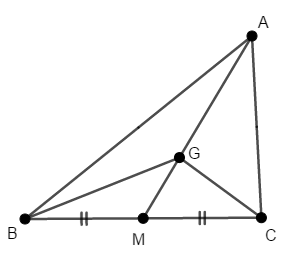
ここから線分の比を利用していけば,\(\triangle\mathrm{GBC}\)などの面積を求められます。 まず\(\triangle\mathrm{AMC}\)の面積を求めます。
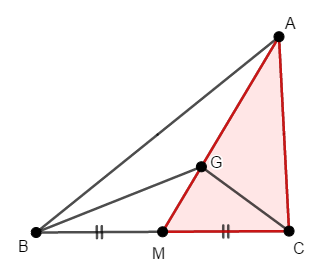
\(\triangle\mathrm{ABM}\)と\(\triangle\mathrm{AMC}\)は,底辺が\(\mathrm{BM} = \mathrm{MC}\)と同じ長さであり,高さも同じです。 ですから両者の面積は同じであり,\(\triangle\mathrm{AMC}\)の面積は次のように求められます。
高さが同じであることを理解しづらかったら,次の図を見てください。 赤い線は両者の三角形に共通する高さです。
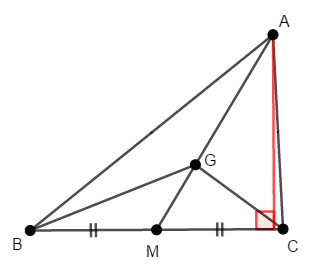
さらに\(\triangle\mathrm{GMC}\)の面積も求められます。 \(\mathrm{AG} : \mathrm{GM} = 2 : 1\)であることに注意します。
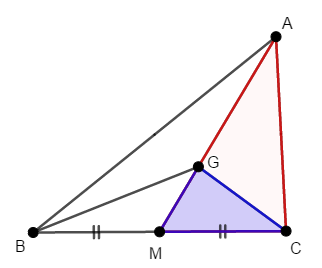
\(\triangle\mathrm{AGC}\)と\(\triangle\mathrm{GMC}\)は,頂点\(\mathrm{C}\)から対辺に下ろした高さが同じであり,底辺の比が\(2 : 1\)です。 なので\(\triangle\mathrm{GMC}\)の面積は次のように求められます。
全く同様の議論で\(\triangle\mathrm{GBM}\)の面積も\(\displaystyle\frac{1}{6}S\)であると分かります。 したがって,\(\triangle\mathrm{GBC}\)の面積は\(\displaystyle\frac{1}{3}S\)です。 同様に\(\triangle\mathrm{GAB}\),\(\triangle\mathrm{GCA}\)の面積も\(\displaystyle\frac{1}{3}S\)です。
以上より,\(\triangle\mathrm{GAB}\),\(\triangle\mathrm{GBC}\),\(\triangle\mathrm{GCA}\)の面積は等しいです。
\(6\)等分の話を経ずに直接\(3\)等分の証明もできます。 辺\(\mathrm{BC}\)の中点を\(\mathrm{M}\)とします。
\(\triangle\mathrm{ABC}\)は\(\triangle\mathrm{GBC}\)と同じ底辺\(\mathrm{BC}\)を持ちます。 したがって,両者の面積の比は高さの比と等しいです。 高さの比を考えるために\(\mathrm{A}\),\(\mathrm{G}\)から辺\(\mathrm{BC}\)にそれぞれ垂線\(\mathrm{AH}_1\),\(\mathrm{GH}_2\)を下ろします。
\(\mathrm{AH}_1 /\!/ \mathrm{GH}_2\)ですから同位角は等しく,\(\angle\mathrm{MAH}_1 = \angle\mathrm{MGH}_2\)です。 したがって,直角三角形\(\triangle\mathrm{MAH}_1\)と\(\triangle\mathrm{MGH}_2\)は\(2\)組の内角がそれぞれ等しいので相似であり,相似比は斜辺の長さの比である\(3 : 1\)です。
対応する辺の比は相似比の通りですから,\(\mathrm{AH}_1 : \mathrm{GH}_2 = 3 : 1\)です。 これは\(\triangle\mathrm{ABC}\)と\(\triangle\mathrm{GBC}\)の高さの比であり,面積の比ですから,\(\triangle\mathrm{GBC} = \displaystyle\frac{1}{3}\triangle\mathrm{ABC}\)です。 \(\triangle\mathrm{GAB}\),\(\triangle\mathrm{GCA}\)についても同様であり,これらの面積は等しいです。
