今回から高校数学の平面図形を扱っていきます。 まずは線分の内分・外分から。 線分の分割を表したり,線分(とその延長上)の点の位置を示したりできます。
目次
内分
線分\(\mathrm{AB}\)上の点\(\mathrm{P}\)を考えます。 この点が線分をどんな比で分割するかを考えると,点の線分上での位置を表現できます。
\(\mathrm{AP} : \mathrm{PB} = m : n\)(\(m\),\(n\)は正の数)であるとき,点\(\mathrm{P}\)は線分\(\mathrm{AB}\)を\(m : n\)に内分するといいます。 またこの点\(\mathrm{P}\)を内分点といいます。
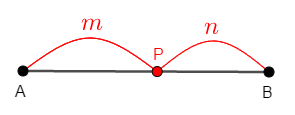
上図の\(m : n\)の比を表すぴょんぴょんした曲線を次のように捉えると,次項の外分も覚えやすいです。
端点\(\mathrm{A}\)から始まって,\(m\)だけ飛んで\(\mathrm{A}\)と\(\mathrm{B}\)の間の点\(\mathrm{P}\)を経由し,\(n\)だけ飛んで端点\(\mathrm{B}\)に着地すると考えます。 比の順番にも意味があり,線分\(\mathrm{BA}\)を\(m : n\)に内分する場合,その内分点は線分\(\mathrm{AB}\)を\(n : m\)に内分する点と同じになります。
外分
線分の外分というものも考えられます。 内分は\(\mathrm{A}\)と\(\mathrm{B}\)の間に点をとりますが,外分は線分\(\mathrm{AB}\)の外側(延長線上)に点をとります。
線分\(\mathrm{AB}\)の\(\mathrm{B}\)側の延長線上にある点\(\mathrm{P}\)を考えます。 この点が\(\mathrm{AP} : \mathrm{PB} = m : n\)(\(m\),\(n\)は正の数)を満たすとき,点\(\mathrm{P}\)は線分\(\mathrm{AB}\)を\(m : n\)に外分するといいます。 またこの点\(\mathrm{P}\)を外分点といいます。
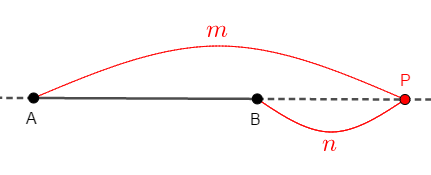
内分の場合と同じく,端点\(\mathrm{A}\)から始まって,\(m\)だけ飛んで\(\mathrm{B}\)を飛び越えた先の点\(\mathrm{P}\)を経由し,\(n\)だけ飛んで端点\(\mathrm{B}\)に戻って着地すると考えます。 当然この場合,\(m > n\)です。
では,\(m < n\)の場合はどうなるでしょうか? \(2\)回目のジャンプの方が大きいのですから,初めに\(\mathrm{B}\)を飛び越えると\(\mathrm{B}\)に戻れなくなります。 この場合は,初めに左に飛ぶのです。
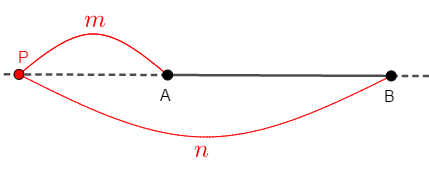
つまり,\(m < n\)の場合の外分点は,線分\(\mathrm{AB}\)の\(\mathrm{A}\)側の延長線上にあります。 \(m\)と\(n\)の大小関係をよく見て,外分点がどちら側にあるか判断できるようにしましょう。
三角形の内角の二等分
内分・外分に関する重要な定理として,三角形の内角・外角の二等分線がその対辺のどこと交わるかという問題があります。
まず三角形の内角の二等分線を考えてみましょう。 \(\triangle\mathrm{ABC}\)の\(\angle\mathrm{A}\)の二等分線と辺\(\mathrm{BC}\)の交点を\(\mathrm{P}\)とします。
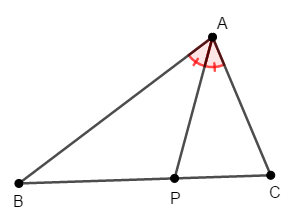
この点\(\mathrm{P}\)は辺\(\mathrm{BC}\)をどう内分するでしょうか? 内分の比を考えるので,三角形の相似を考え,その相似比を求めると良いです。
しかしこの場合,三角形の相似を直接考えなくても,平行線と線分の比を利用できます。 \(\mathrm{BP} : \mathrm{PC}\)の部分からそれを連想するのです。
平行線と線分の比を考えるために,頂点\(\mathrm{C}\)を通って\(\mathrm{AP}\)と平行な線分\(\mathrm{CX}\)を考えます。 点\(\mathrm{X}\)は辺\(\mathrm{AB}\)の延長線上にとります。
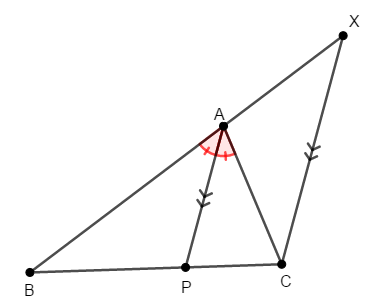
これで平行線と線分の比を考える準備が整いました。 求めたいのは内分の比\(\mathrm{BP} : \mathrm{PC}\)ですから,その比を考えると,次が成り立ちます。
まだ\(\mathrm{AX}\)が何者かよく分かりませんから,もう少し考えます。 せっかく平行線を引いたので,等しい同位角・錯角を見つけましょう。
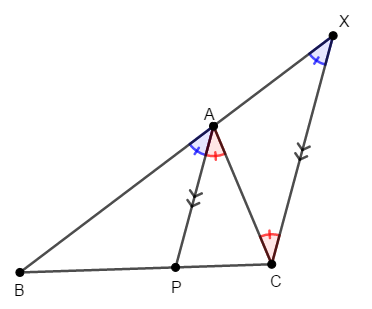
青い角同士は同位角,赤い角同士は錯角で等しいです。 これで\(\triangle\mathrm{ACX}\)は底角が等しいので二等辺三角形であり,\(\mathrm{AX} = \mathrm{AC}\)であることが分かります。 これで先ほど求めた比は次のようになります。
つまり,三角形の内角の二等分線と対辺の交点は,対辺をその角と隣り合う\(2\)辺の比で内分するわけです。
\(\triangle\mathrm{ABC}\)の\(\angle\mathrm{A}\)の二等分線と辺\(\mathrm{BC}\)の交点を\(\mathrm{P}\)とする。 このとき,点\(\mathrm{P}\)は辺\(\mathrm{BC}\)を\(\mathrm{AB} : \mathrm{AC}\)に内分する。
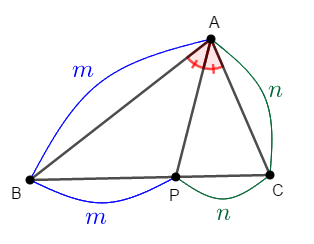
平面図形では角の二等分線をよく考えますから,この定理の使い道も多いです。 よく覚えておきましょう。
三角形の外角の二等分
次は三角形の外角の二等分線を考えます。 \(\triangle\mathrm{ABC}\)の頂点\(\mathrm{A}\)での外角の二等分線と辺\(\mathrm{BC}\)の延長線の交点を\(\mathrm{P}\)とします。
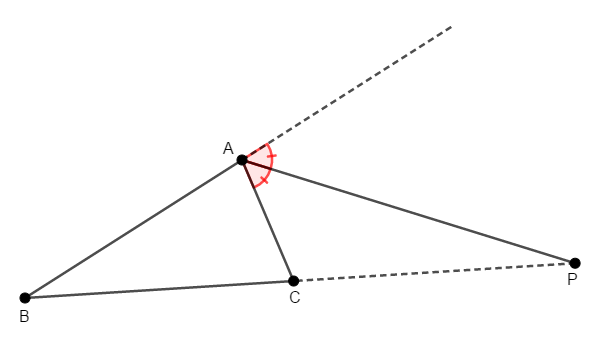
この点\(\mathrm{P}\)が線分\(\mathrm{BC}\)をどんな比で外分するか考えましょう。 図のように\(\mathrm{AB} > \mathrm{AC}\)の場合だけ考えます。
\(\mathrm{AB} < \mathrm{AC}\)の場合は,点\(\mathrm{P}\)の位置が反対側(辺\(\mathrm{BC}\)の\(\mathrm{B}\)側の延長線上)に変わりますが,\(\mathrm{AB} > \mathrm{AC}\)の場合と同じ議論になります。
\(\mathrm{AB} = \mathrm{AC}\)の場合は,\(\mathrm{A}\)の外角の二等分線と辺\(\mathrm{BC}\)が平行になり,交点が現われません。 平行になるのは,同位角・錯角が等しいことを示すことができるからです。
この場合,下図のように外角を二等分した角はそれぞれ等しく,三角形の底角もそれぞれ等しいです。 そしてそのどちらも,角度は\((180^{\circ} - \angle\mathrm{A}) \div 2\)です。
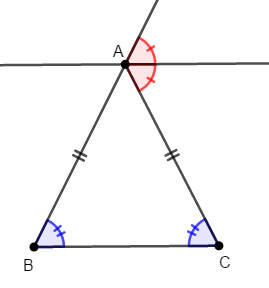
したがって,同位角・錯角が等しいことが分かったので,\(\mathrm{A}\)の外角の二等分線と辺\(\mathrm{BC}\)は平行です。
内角の二等分線を考えたときと同じく,頂点\(\mathrm{C}\)を通って\(\mathrm{AP}\)と平行な線分\(\mathrm{CX}\)を考えます。 点\(\mathrm{X}\)は辺\(\mathrm{AB}\)上にとります。
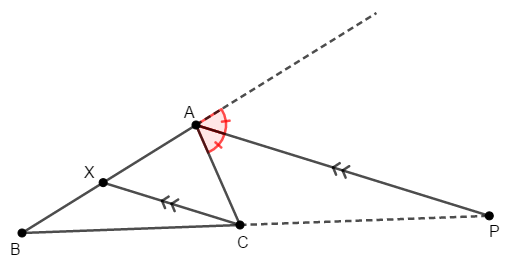
これで平行線と線分の比を考えられます。 求めたいのは外分の比\(\mathrm{BP} : \mathrm{PC}\)ですから,その比を考えると,次が成り立ちます。
平行線と線分の比を学んだときには,この比の式は出てこなかったかもしれません。 しかし少し考えれば,この式が成り立つことが分かります。 次の比の式が成り立つことは習いましたね。
この式から,\(\mathrm{BC} = a\),\(\mathrm{BX} = b\)とすると,定数\(k\)(\(> 1\))を用いて\(\mathrm{BP} = ka\),\(\mathrm{BA} = kb\)と表せます。 よって,\(\mathrm{CP} = (k - 1)a\),\(\mathrm{XA} = (k - 1)b\)と表せます。 したがって,次の比の式が成り立つわけです。
まだ\(\mathrm{AX}\)が何者かよく分かりませんから,もう少し考えます。 せっかく平行線を引いたので,等しい同位角・錯角を見つけましょう。
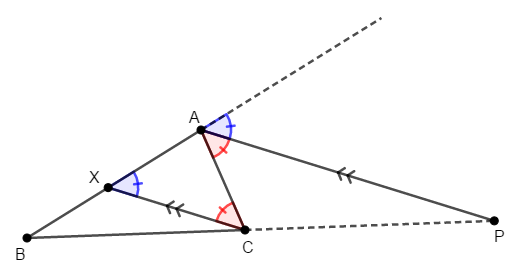
青い角同士は同位角,赤い角同士は錯角で等しいです。 これで\(\triangle\mathrm{ACX}\)は底角が等しいので二等辺三角形であり,\(\mathrm{AX} = \mathrm{AC}\)であることが分かります。 これで先ほど求めた比は次のようになります。
つまり,三角形の外角の二等分線と対辺(の延長線)の交点は,対辺をその角と隣り合う\(2\)辺の比で外分するわけです。
\(\mathrm{AB} \neq \mathrm{AC}\)である\(\triangle\mathrm{ABC}\)の頂点\(\mathrm{A}\)での外角の二等分線と辺\(\mathrm{BC}\)の延長線の交点を\(\mathrm{P}\)とする。 このとき,点\(\mathrm{P}\)は辺\(\mathrm{BC}\)を\(\mathrm{AB} : \mathrm{AC}\)に外分する。
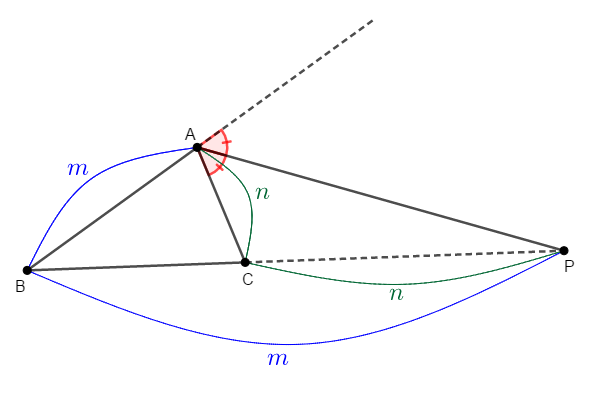
これは\(\mathrm{AB} < \mathrm{AC}\)の場合にも成り立ちます。 この場合の外分点は,辺\(\mathrm{BC}\)の\(\mathrm{B}\)側の延長線上にあります。
確認問題
\(\mathrm{AB} = 7\),\(\mathrm{BC} = 6\),\(\mathrm{CA} = 9\)である\(\triangle\mathrm{ABC}\)を考えます。 頂点\(\mathrm{A}\)での内角の二等分線と辺\(\mathrm{BC}\)との交点を\(\mathrm{P}\),外角の二等分線と辺\(\mathrm{BC}\)の延長線との交点を\(\mathrm{Q}\)とします。
このとき,線分\(\mathrm{PQ}\)の長さを求めてください。
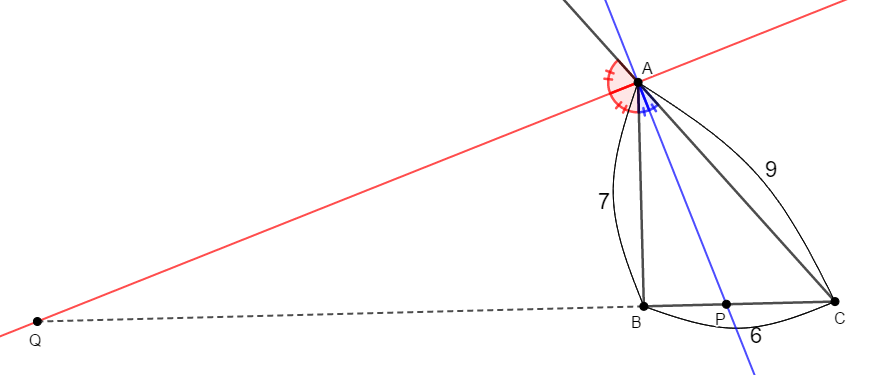
答え
直線\(\mathrm{AP}\)は\(\angle\mathrm{A}\)の二等分線ですから,点\(\mathrm{P}\)が辺\(\mathrm{BC}\)を内分する比は次のように分かります。
したがって,\(\mathrm{BP}\)は次のように求められます。
また,直線\(\mathrm{AQ}\)は頂点\(\mathrm{A}\)での外角の二等分線ですから,点\(\mathrm{Q}\)が辺\(\mathrm{BC}\)を外分する比は次のように分かります。
したがって,\(\mathrm{BQ} = x\)とすると,\(x\)は次のように求められます。
以上より,\(\mathrm{PQ}\)は次のように求められます。
下図のように\(\triangle\mathrm{ABC}\)の各角の二等分線を引き,それぞれの対辺との交点\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)をとります。 \(\mathrm{BC} = a\),\(\mathrm{CA} = b\),\(\mathrm{AB} = c\)とし,\(\triangle\mathrm{ABC}\)の面積を\(S\)とします。 (1)~(3)に答えてください。
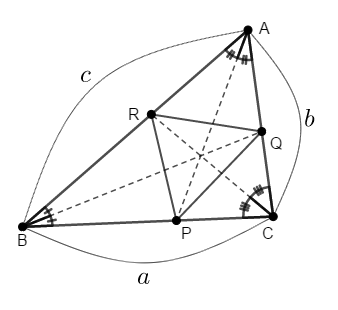
-
\(\triangle\mathrm{ABP}\)の面積を\(a\),\(b\),\(c\),\(S\)で表してください。
-
\(\triangle\mathrm{BRP}\)の面積を\(a\),\(b\),\(c\),\(S\)で表してください。
-
\(\triangle\mathrm{PQR}\)の面積を\(a\),\(b\),\(c\),\(S\)で表してください。
答え
面積比を考える問題です。 三角形の面積比を求める問題はよくありますが,大抵は面積そのものを求める必要はありません。
三角形の面積は「底辺\(\times\)高さ\(\div 2\)」で求められますから,底辺が等しい三角形の面積比は高さの比と等しいですし,高さが等しい三角形の面積比は底辺の比と等しいです。
-
三角形の角の二等分線を考えていますから,各辺がどんな比で内分されているかが分かります。 図に書き込んでおきましょう。
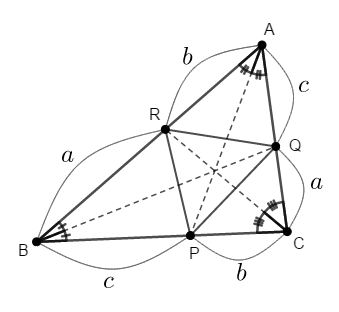
目的は\(\triangle\mathrm{ABP}\)の面積を考えることですが,頂点\(\mathrm{A}\)から垂線を下ろして高さとすることを考えると,実は\(\triangle\mathrm{ABP}\)と\(\triangle\mathrm{ABC}\)の高さは全く同じです。 なのでこれらの面積比は底辺の比に等しいです。
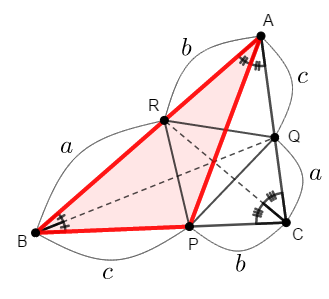
\(\mathrm{BP} : \mathrm{PC} = c : b\)ですから,底辺の比を考えると,\(\triangle\mathrm{ABP}\)の面積は次のようになります。
\( \begin{align} \triangle\mathrm{ABP} &= \displaystyle\frac{c}{b + c} \triangle\mathrm{ABC} \\[5pt] &= \textcolor{red}{\displaystyle\frac{c}{b + c}S} \end{align} \) -
前問と同様に考えます。 頂点\(\mathrm{P}\)から垂線を下ろして高さとすると,\(\triangle\mathrm{BRP}\)と\(\triangle\mathrm{ABP}\)の高さは同じです。 したがって,面積比は底辺の比に等しいです。
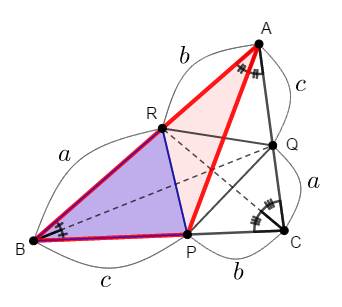
\(\mathrm{BR} : \mathrm{RA} = a : b\)ですから,底辺の比を考えると,\(\triangle\mathrm{BRP}\)の面積は次のようになります。
\( \begin{align} \triangle\mathrm{BRP} &= \displaystyle\frac{a}{a + b} \triangle\mathrm{ABP} \\[5pt] &= \displaystyle\frac{a}{a + b} \cdot \displaystyle\frac{c}{b + c}S \\[5pt] &= \textcolor{red}{\displaystyle\frac{ca}{(a + b)(b + c)}S} \end{align} \) -
(1),(2)と同様に考えると,\(\triangle\mathrm{AQR}\),\(\triangle\mathrm{CPQ}\)の面積も分かります。
\(\triangle\mathrm{AQR}\)を求めるときはまず\(\triangle\mathrm{ABQ}\)から考え,\(\triangle\mathrm{CPQ}\)を求めるときはまず\(\triangle\mathrm{ACP}\)から考えます。 底辺の比を考えれば,それぞれの面積は次のようになると分かります。
\( \begin{align} \triangle\mathrm{AQR} &= \displaystyle\frac{bc}{(a + b)(c + a)}S \\[5pt] \triangle\mathrm{CPQ} &= \displaystyle\frac{ab}{(b + c)(c + a)}S \end{align} \)\(\triangle\mathrm{PQR}\)は\(\triangle\mathrm{ABC}\)から\(\triangle\mathrm{AQR}\),\(\triangle\mathrm{BRP}\),\(\triangle\mathrm{CPQ}\)を除いたものですから,これでその面積が分かります。
\( \begin{align} &\quad\triangle\mathrm{PQR} \\[5pt] &= \triangle\mathrm{ABC} - \triangle\mathrm{AQR} - \triangle\mathrm{BRP} - \triangle\mathrm{CPQ} \\[5pt] &= S - \displaystyle\frac{bc}{(a + b)(c + a)}S - \displaystyle\frac{ca}{(a + b)(b + c)}S - \displaystyle\frac{ab}{(b + c)(c + a)}S \\[5pt] &= \left\{ 1 - \displaystyle\frac{bc}{(a + b)(c + a)} - \displaystyle\frac{ca}{(a + b)(b + c)} - \displaystyle\frac{ab}{(b + c)(c + a)} \right\} S \\[5pt] &= \displaystyle\frac{(a + b)(b + c)(c + a) - ab(a + b) - bc(b + c) - ca(c + a)}{(a + b)(b + c)(c + a)}S \\[5pt] &= \textcolor{red}{\displaystyle\frac{2abc}{(a + b)(b + c)(c + a)}S} \end{align} \)最後の分子の計算は素直にやると面倒ですが,\((a + b)(b + c)(c + a)\)を展開して出てくる項をよく考えると簡単です。 まず\(abc\)は\(2\)回だけ出てきます。 その他の項は\(a\),\(b\),\(c\)のうち\(2\)種類だけの積からなる項ですが,それらは全て\((a + b)(b + c)(c + a)\)の後ろの項に打ち消されます。
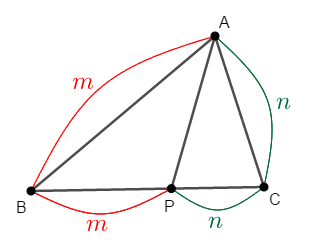
\(\triangle\mathrm{ABC}\)の辺\(\mathrm{BC}\)上の点\(\mathrm{P}\)が次の式を満たすとき,線分\(\mathrm{AP}\)が\(\angle\mathrm{A}\)を二等分することを証明してください。
答え
\(\mathrm{AB} : \mathrm{AC} = m : n\)とすると,問題の条件を下図のように表せます。
証明方法はざっくり\(2\)通りあります。 順に見ていきましょう。
まずは短い証明です。
\(\angle\mathrm{A}\)の二等分線と辺\(\mathrm{BC}\)の交点を\(\mathrm{Q}\)とし,点\(\mathrm{P}\)と点\(\mathrm{Q}\)が一致することを示します。 点\(\mathrm{Q}\)については,次の比が成り立ちます。
問題文の条件より\(\mathrm{BP} : \mathrm{PC} = m : n\)ですから,次が成り立ちます。
よって,点\(\mathrm{P}\),\(\mathrm{Q}\)は辺\(\mathrm{BC}\)を同じ比で内分しているため,同一の点です。 したがって,線分\(\mathrm{AP}\)は\(\angle\mathrm{A}\)を二等分します。
もうひとつの証明は,より正攻法的な方法です。 本文でこの問題の逆を証明しましたが,その手順を再利用します。
頂点\(\mathrm{C}\)を通り線分\(\mathrm{AP}\)と平行な線分\(\mathrm{CX}\)を引きます。 ただし点\(\mathrm{X}\)は辺\(\mathrm{AB}\)の延長上にとります。
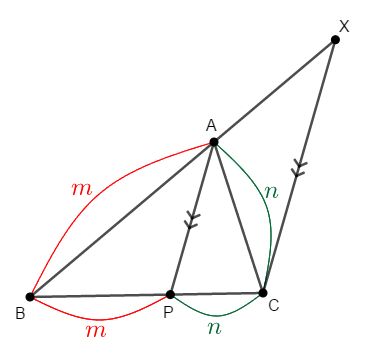
ここで,\(\mathrm{AP} /\!/ \mathrm{XC}\)であることから,平行線と線分の比の関係より,次が成り立ちます。
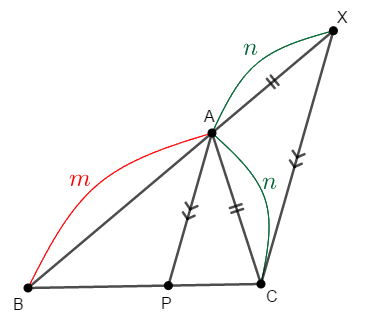
線分\(\mathrm{AB}\)の長さを\(m\)としたときの線分\(\mathrm{AX}\),\(\mathrm{AC}\)の長さがともに\(n\)なのですから,\(\triangle\mathrm{ACX}\)は二等辺三角形です。 したがって,その底角は等しいです。
また,\(\mathrm{AP} /\!/ \mathrm{XC}\)であることから,同位角である\(\angle\mathrm{BAP}\)と\(\angle\mathrm{BXC}\)が等しく,錯角である\(\angle\mathrm{PAC}\)と\(\angle\mathrm{ACX}\)が等しいです。
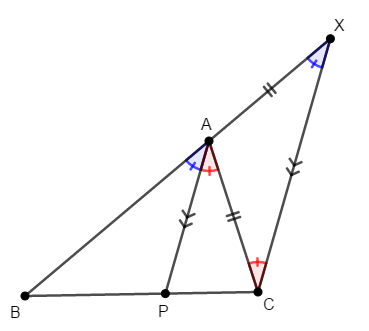
したがって,次が成り立ちます。
以上より,線分\(\mathrm{AP}\)は\(\angle\mathrm{A}\)を二等分します。
