前回学んだ三角形の外心・内心・重心と同じく,三角形の五心である垂心・傍心についても学びます。
目次
垂心
前回学んだ通り,三角形の辺の垂直二等分線\(3\)本や角の二等分線\(3\)本,中線\(3\)本は共点でした。 それぞれの交点を外心,内心,重心といいました。
同様に,三角形の各頂点から対辺に下ろした垂線\(3\)本も共点です。
三角形の各頂点から対辺に下ろした垂線は\(1\)点で交わる。 この共有点をこの三角形の垂心と呼ぶ。
さっそく証明してみましょう。 \(\mathrm{A}\),\(\mathrm{B}\),\(\mathrm{C}\)から対辺に下ろした垂線をそれぞれ\(\mathrm{X}\),\(\mathrm{Y}\),\(\mathrm{Z}\)とします。
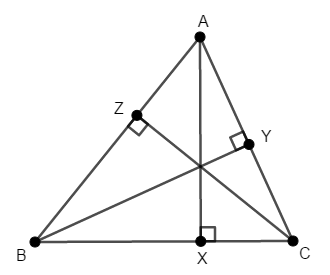
共点を示す方針はいくつかありますが,ここでは変わった方法をとります。 前回,三角形の各辺の垂直二等分線が共点であることを証明しました。 この交点は外心でしたね。
今回は二等分線ではありませんが,垂線であることは共通なので,垂直二等分線が共点であることを利用する方法があります。 つまり垂心が,ある三角形の外心になることを示すのです。
そのために,次のように各辺と平行で,その辺の向かい側の頂点を通る直線を引きます。 それらの交点を次図のように\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)とします。
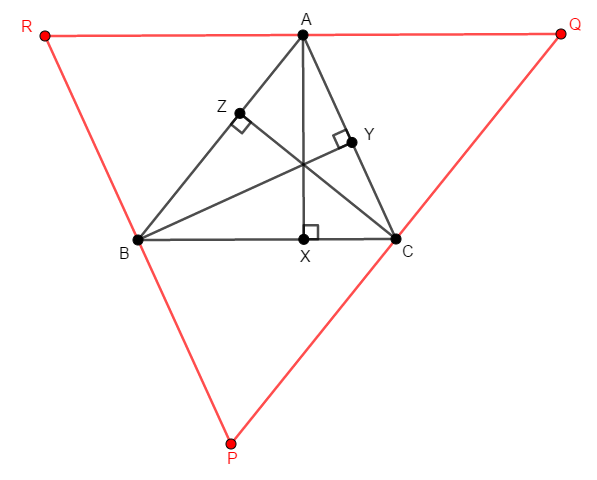
なぜこんな補助線を引くのかは,少し議論を進めればすぐ分かります。 このとき,四角形\(\mathrm{ABCQ}\)などの平行四辺形ができますね。
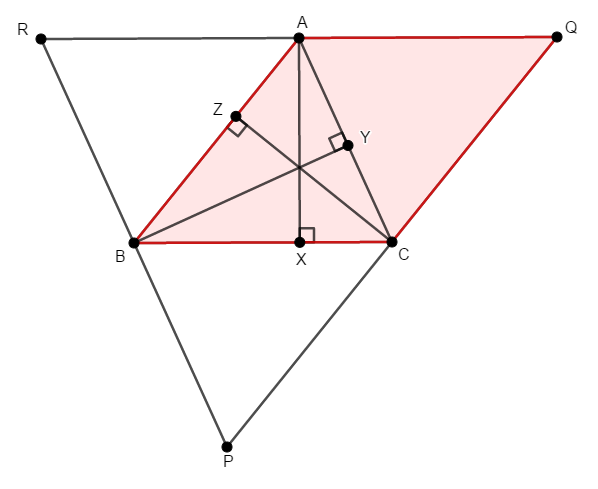
平行四辺形の対辺は同じ長さですから,\(\mathrm{AB} = \mathrm{QC}\),\(\mathrm{AQ} = \mathrm{BC}\)です。
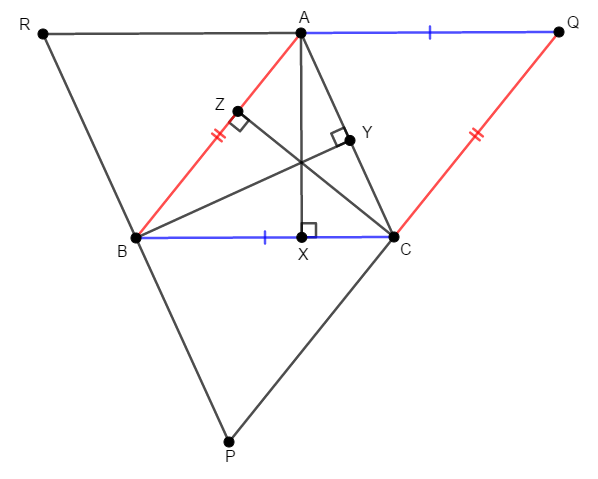
同様に四角形\(\mathrm{RBCA}\),\(\mathrm{ABPC}\)も平行四辺形ですから,その対辺の長さは等しく,次図のように長さの等しい線分が見つかります。
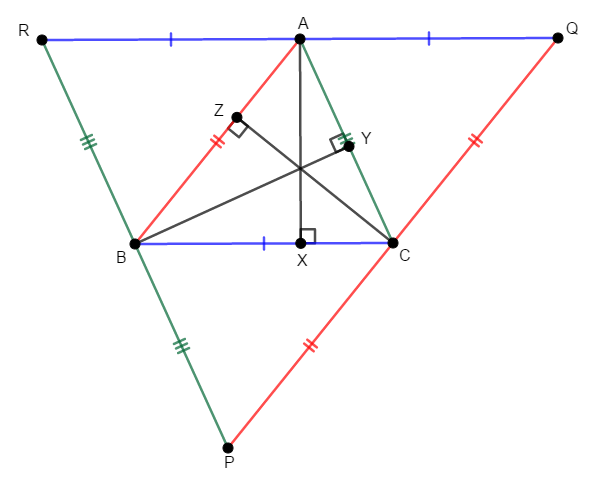
これで先ほどの補助線の意図が見えてきましたか? 各垂線が何らかの三角形の垂直二等分線であれば,前回学んだ通り,それは共点だということになりますね。
その状況を作るために,各頂点の両側に長さの等しい線分を置き,新しい三角形\(\mathrm{PQR}\)を作ったわけです。 なぜ補助線を辺と平行に引いたかというと,垂線の「直角」を受け継ぐためです。 平行であれば錯角が等しいので,次が成り立つことが分かります。
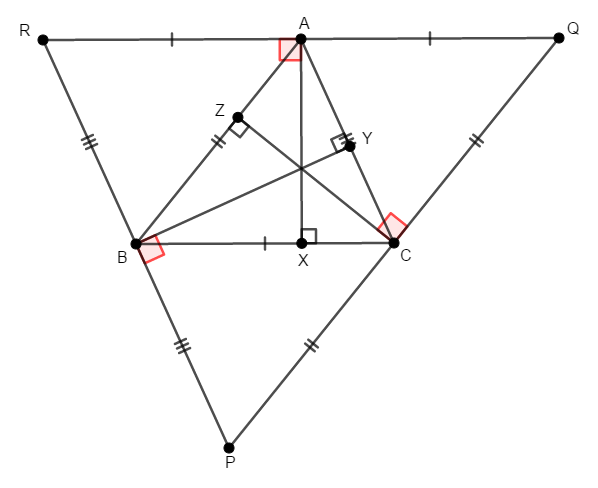
これで正真正銘,\(\mathrm{AX}\)は辺\(\mathrm{RQ}\)の,\(\mathrm{BY}\)は辺\(\mathrm{RP}\)の,\(\mathrm{CZ}\)は辺\(\mathrm{PQ}\)の垂直二等分線になります。 したがって各垂線\(\mathrm{AX}\),\(\mathrm{BY}\),\(\mathrm{CZ}\)は共点であり,その交点は\(\triangle\mathrm{PQR}\)の外心です。
思い付くわけのない補助線を引くな!と思うかもしれませんが,実は上記の通り,先を見越した意図的な補助線なのです。 欲しい状況をつくるために引くのが補助線です。
傍心
五心の最後の\(1\)つは傍心です。
三角形の\(1\)つの頂点での内角の二等分線と,他の\(2\)頂点での外角の二等分線は\(1\)点で交わる。 この共有点をこの三角形の傍心と呼ぶ。
角の二等分線の交点という点では,内心と似ていますね。 内心と同じく,傍心も三角形に関するとある円の中心です。 その円を傍接円といい,三角形の\(1\)辺と他の\(2\)辺の延長線に接する円です。
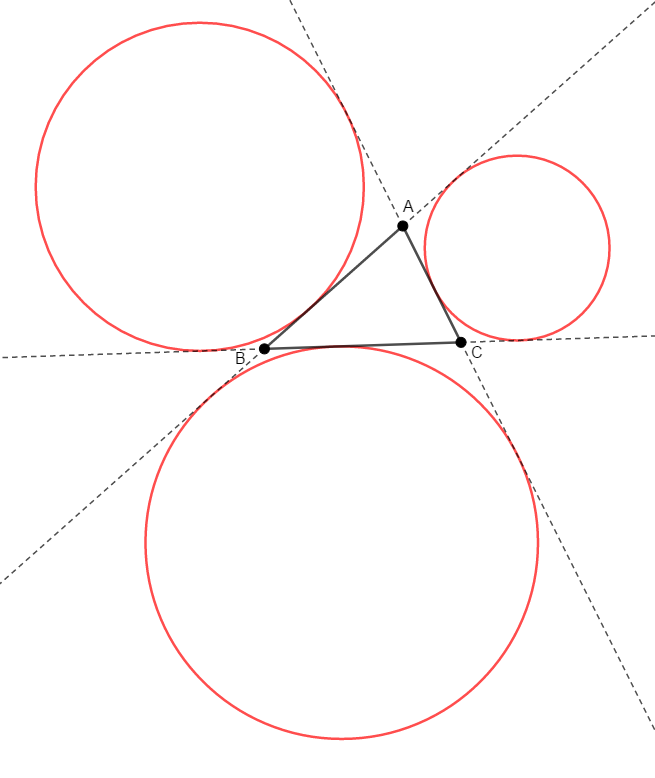
図の通り,三角形の傍心・傍接円は\(3\)つあり,例えば内角\(\angle\mathrm{A}\)の二等分線上にある傍心を「\(\angle\mathrm{A}\)内の傍心」といいます。 では,これらの二等分線が共点であることと,この共有点(傍心)が傍接円の中心であることを証明しましょう。
交点を示す方針はいくつかありますが,\(2\)直線の交点が,残りの直線上の点でもあることを証明します。 具体的には,まず外角の二等分線の交点を考え,その点が他の内角の二等分線上にあることを証明します。
\(\angle\mathrm{B}\),\(\angle\mathrm{C}\)での外角の二等分線の交点を\(\mathrm{P}\)とします。
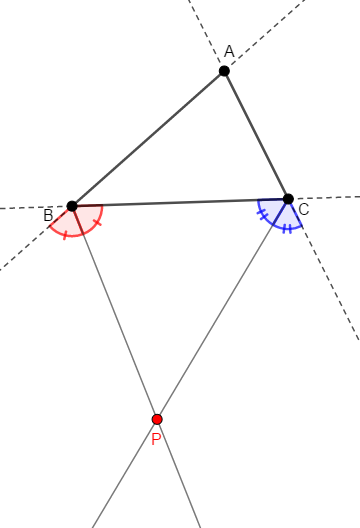
証明すべきことは次の\(2\)点です。
- 点\(\mathrm{P}\)が\(\angle\mathrm{A}\)の二等分線上にあることを示せば,各二等分線が共点であることが分かる。
- 点\(\mathrm{P}\)と各辺(とその延長線)への距離が等しいことを示せば,この共有点が傍接円の中心であることが分かる。
これらを考えるため,各辺(とその延長線)への垂線(緑色)と線分\(\mathrm{AP}\)(赤色)を次のように引きます。
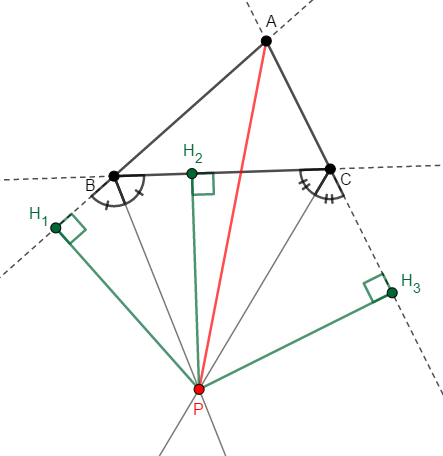
\(1\)点目を証明するには,\(\angle\mathrm{BAP} = \angle\mathrm{CAP}\)を示す必要があります。 角度が等しいことの証明には三角形の相似(合同)を活用できますから,まず\(2\)点目を証明することで三角形の相似(合同)を見つける材料を増やしましょう。
角の二等分線上の点が角をなす\(2\)直線と等距離にあることは,前回説明した通りです。 点\(\mathrm{P}\)は\(\angle\mathrm{H}_1\mathrm{BH}_2\)の二等分線上の点ですから,次が成り立ちます。
前回学んだことを思い出せなくても,三角形の合同を考えれば上の式は分かります。 \(\triangle\mathrm{PBH}_1\)と\(\triangle\mathrm{PBH}_2\)が,斜辺と\(1\)つの鋭角がそれぞれ等しいから合同ですね。 対応する辺が等しいことから,上の式が成り立ちます。
同様に点\(\mathrm{P}\)は\(\angle\mathrm{H}_2\mathrm{CH}_3\)の二等分線上の点でもありますから,次も成り立ちます。
これらの式から\(\mathrm{PH}_1 = \mathrm{PH}_3\)が成り立ちます。 したがって,点\(\mathrm{P}\)は三角形の各辺(とその延長線)と等距離にあり,これが傍接円の中心になっていることが分かりました。
同時に,この式から点\(\mathrm{P}\)が\(\mathrm{AH}_1\),\(\mathrm{AH}_3\)と等距離にあるため,\(\angle\mathrm{H}_1\mathrm{AH}_3\),つまり\(\angle\mathrm{A}\)の二等分線上にあることが分かります。 \(\triangle\mathrm{PAH}_1\)と\(\triangle\mathrm{PAH}_3\)が合同であることから証明しても良いですね。
これで示すべき\(2\)点を示せました。 これは傍心の\(1\)つについての証明ですが,当然他の傍心についても成り立つ議論です。
これまで学んだ外心・内心・重心・垂心・傍心を三角形の五心といいます。 それぞれの定義や性質を理解しておきましょう。
確認問題
\(\triangle\mathrm{ABC}\)が鋭角三角形(全ての内角が鋭角)であるとき,その垂心\(\mathrm{H}\)は三角形の内部にあります。 このとき,次の式が成り立つことを証明してください。
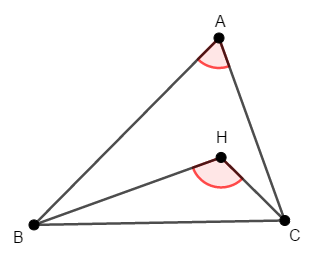
答え
「垂心」という情報を利用するために,線分\(\mathrm{BH}\),\(\mathrm{CH}\)をそれぞれ辺\(\mathrm{CA}\),\(\mathrm{AB}\)まで延長し,その交点をそれぞれ\(\mathrm{P}\),\(\mathrm{Q}\)とすると,これは垂線になります。
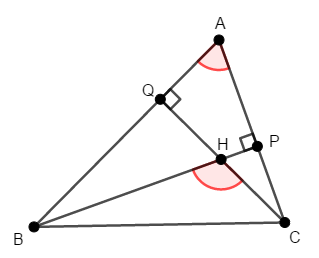
したがって,四角形\(\mathrm{APHQ}\)の内角の和が\(360^{\circ}\)であることに注目すると,次の式が成り立ちます。
対頂角が等しいことから\(\angle\mathrm{PHQ} = \angle\mathrm{BHC}\)なので,次の式が成り立つことが分かります。
\(\triangle\mathrm{ABC}\)の内心を\(\mathrm{I}\)とします。 また,\(\angle\mathrm{A}\)内,\(\angle\mathrm{B}\)内,\(\angle\mathrm{C}\)内の傍心をそれぞれ\(\mathrm{P}\),\(\mathrm{Q}\),\(\mathrm{R}\)とします。
このとき,\(\triangle\mathrm{PQR}\)の垂心が\(\mathrm{I}\)であることを証明してください。
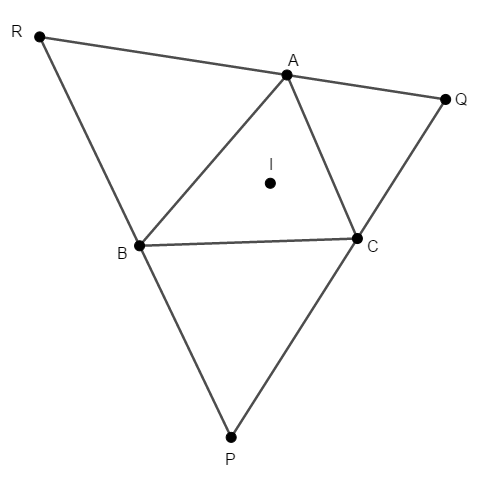
答え
結論から逆算して考えると,\(\triangle\mathrm{PQR}\)の各頂点と\(\mathrm{I}\)を結ぶ直線は,対辺と垂直に交わる必要がありますね。 そのような直線を引いて,実際にそうなることを確かめましょう。
ここで,\(\triangle\mathrm{ABC}\)の\(\angle\mathrm{X}\)の内角の二等分線上には,内心\(\mathrm{I}\)と\(\angle\mathrm{X}\)内の傍心の両方があることに注意します。 例えば\(\mathrm{A}\),\(\mathrm{I}\),\(\mathrm{P}\)は一直線上に並びます。
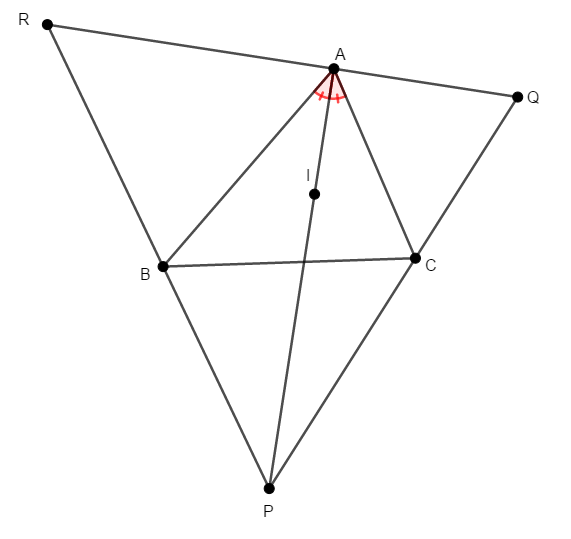
したがって,\(\triangle\mathrm{PQR}\)の各頂点と\(\mathrm{I}\)を結ぶ直線は,いずれも\(\triangle\mathrm{ABC}\)の内角の二等分線であるため,それらが\(\triangle\mathrm{ABC}\)の内心\(\mathrm{I}\)の\(1\)点で交わることが分かります。
あとは\(\angle\mathrm{PAR}\),\(\angle\mathrm{QBP}\),\(\angle\mathrm{RCQ}\)が直角であることが分かれば,\(\mathrm{I}\)が\(\triangle\mathrm{PQR}\)の各頂点から対辺に引いた垂線の交点,すなわち垂心であることが分かります。
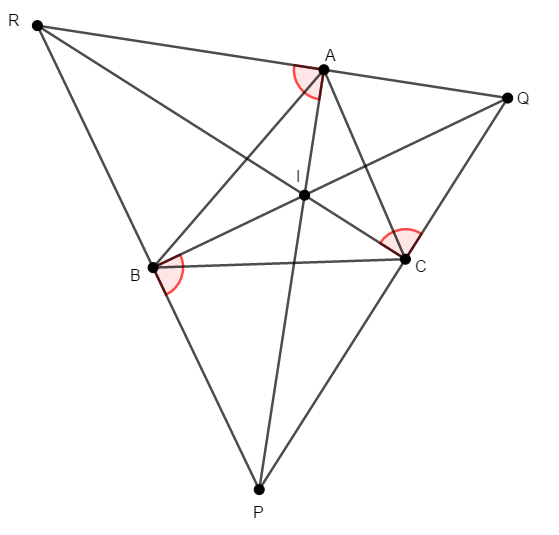
例えば\(\angle\mathrm{PAR}\)を考えると,\(\triangle\mathrm{ABC}\)の\(\angle\mathrm{A}\)での内角の二等分線上に\(\mathrm{P}\),外角の二等分線上に\(\mathrm{Q}\),\(\mathrm{R}\)があるため,次が成り立つことが分かります。
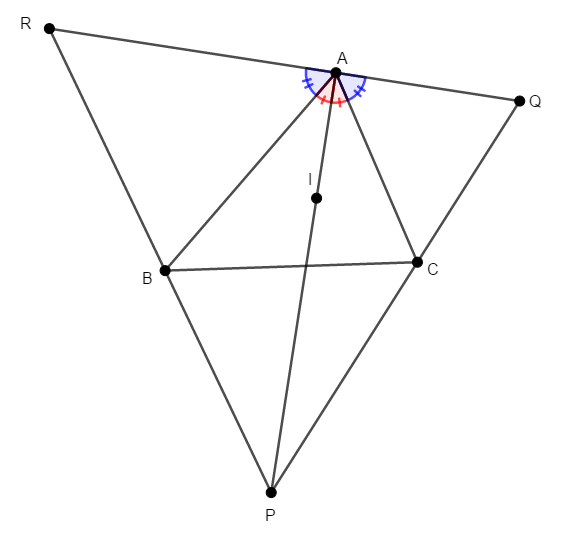
したがって,次が成り立ちます。
これで\(\angle\mathrm{PAR}\)が直角であることが分かりました。 同様に\(\angle\mathrm{QBP}\),\(\angle\mathrm{RCQ}\)も直角であることが分かります。
したがって,\(\triangle\mathrm{PQR}\)の垂心は\(\mathrm{I}\)です。
