２次関数の決定

はじめに

今までは主に，与えられた２次関数について考えてきました。今回は，ある条件を満たす２次関数を見つける練習をします。

２次関数の表し方

▼

今回は，条件を満たす２次関数を見つける練習をします。そのために，まずは２次関数の表し方を確認しておきましょう。２次関数の表し方には，次の３つがあります。

２次関数の表し方

　一般形
\(\quad \quad y = ax^2 + bx + c\)
　頂点が\((p, q)\)
\(\quad \quad y = a(x - p)^2 + q\)
　\(x\)切片の\(x\)座標が\(\alpha, \beta\)
\(\quad \quad y = a(x - \alpha)(x - \beta)\)

色んな表し方がありますね。状況に応じて使いやすい形で表せば，計算が楽になります。次項から詳しく見ていきましょう。

一般形

▲

▼

まずは２次関数の一般的な表し方から確認します。２次関数は，２次式の関数ですから，以下の形で表せましたね。

\( \begin{align} y = ax^2 + bx + c \end{align} \)

具体的な式を求めるには，\(a, b, c\)３つの未知数を求める必要があります。関数のグラフが通る点が３つ分かっていれば，方程式が３つ得られ，３つの未知数が分かるようになります。

例えば，「グラフが３点\((0, 3), (1, 6), (2, 11)\)を通る２次関数を求めよ」という問題を考えてみましょう。ひとまず２次関数を次のように表しておいて，\(a, b, c\)を求めましょう。

\( \begin{align} y = ax^2 + bx + c \end{align} \)

このグラフが上記３点を通るわけですから，\(x, y\)にそれぞれの点の座標を代入した式が成り立ちます。

\( \begin{eqnarray} \left\{ \begin{array}{l} 3 &= a \cdot 0^2 + b \cdot 0 + c \\ 6 &= a \cdot 1^2 + b \cdot 1 + c \\ 11 &= a \cdot 2^2 + b \cdot 2 + c \\ \end{array} \right. \end{eqnarray} \)

式を整理すると，次のようになります。

\( \begin{eqnarray} \left\{ \begin{array}{l} c &= 3 \\ a + b + c &= 6 \\ 4a + 2b + c &= 11 \\ \end{array} \right. \end{eqnarray} \)

この連立方程式を解くと，\((a, b, c) = (1, 2, 3)\)と求められます。これで，この２次関数が次の式で表されることが分かりました。

\( \begin{align} y = x^2 + 2x + 3 \end{align} \)

このように，２次関数のグラフが通る点が３つ分かっているときは，この表し方が便利です。

頂点が分かる場合

▲

▼

２次関数の式を平方完成すると，頂点の座標が一目で分かるようになりました。頂点の座標を\((p, q)\)とすると，２次関数は次のように表せます。

\( \begin{align} y = a(x - p)^2 + q \end{align} \)

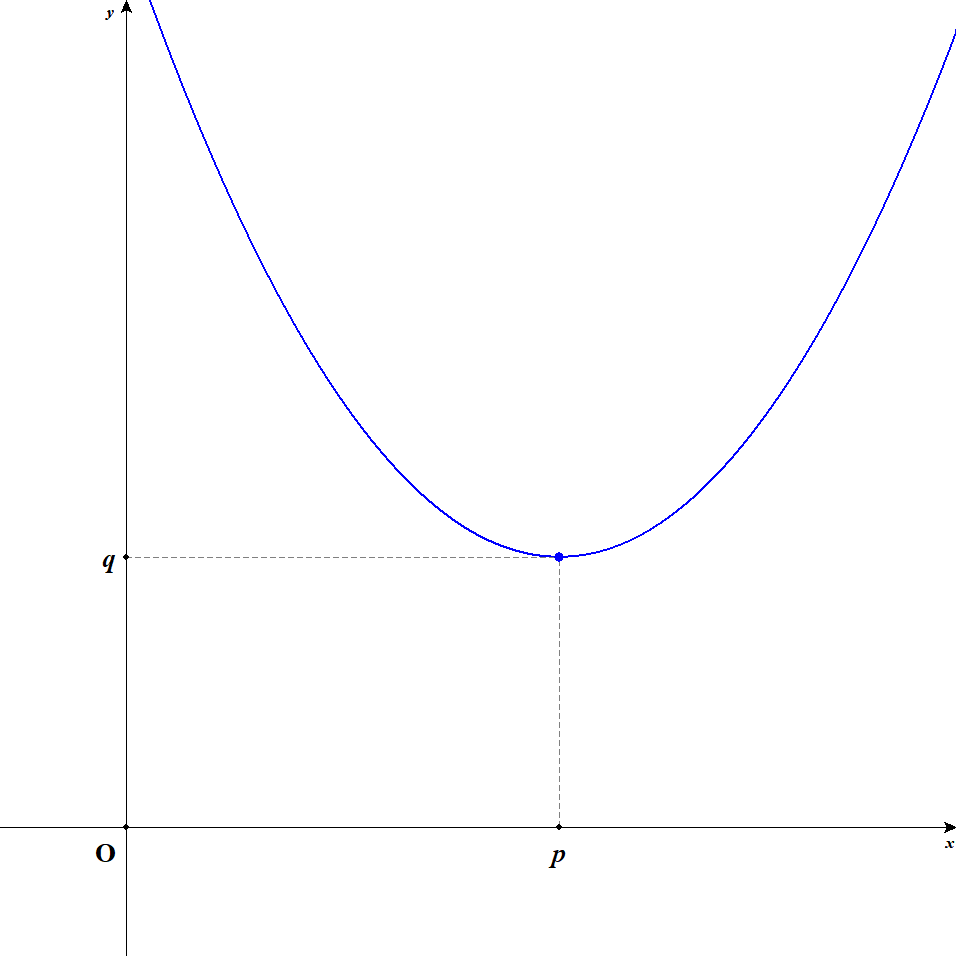
頂点が分かっているときには，未知数は\(a\)ひとつだけですね。

例えば，「グラフの頂点が\((1, 1)\)であり，点\((2, 5)\)を通る２次関数を求めよ」という問題を考えてみましょう。グラフの頂点が分かっているので，２次関数の式は次のように表せます。

\( \begin{align} y = a(x - 1)^2 + 1 \end{align} \)

このグラフが点\((2, 5)\)を通るので，その座標を\(x, y\)に代入すれば，\(a\)を求められます。

\( \begin{align} 5 = a (2 - 1)^2 + 1 \end{align} \)

式を整理することで\(a = 4\)と求められ，この２次関数が次の式で表されることが分かりました。

\( \begin{align} y = 4(x - 1)^2 + 1 \end{align} \)

このように，２次関数のグラフの頂点が分かっているときは，この表し方が便利です。

\(x\)切片が分かる場合

▲

▼

最後に\(x\)切片を使った表し方を紹介します。 \(x\)切片は，２次関数のグラフが\(x\)軸とぶつかる点ですね。詳しくは次回以降で学びますが，\(x\)切片は０～２個あります。

まず\(x\)切片が２つある場合を考え，その\(x\)座標を\(\alpha, \beta\)としましょう。グラフが次のようになる場合です。

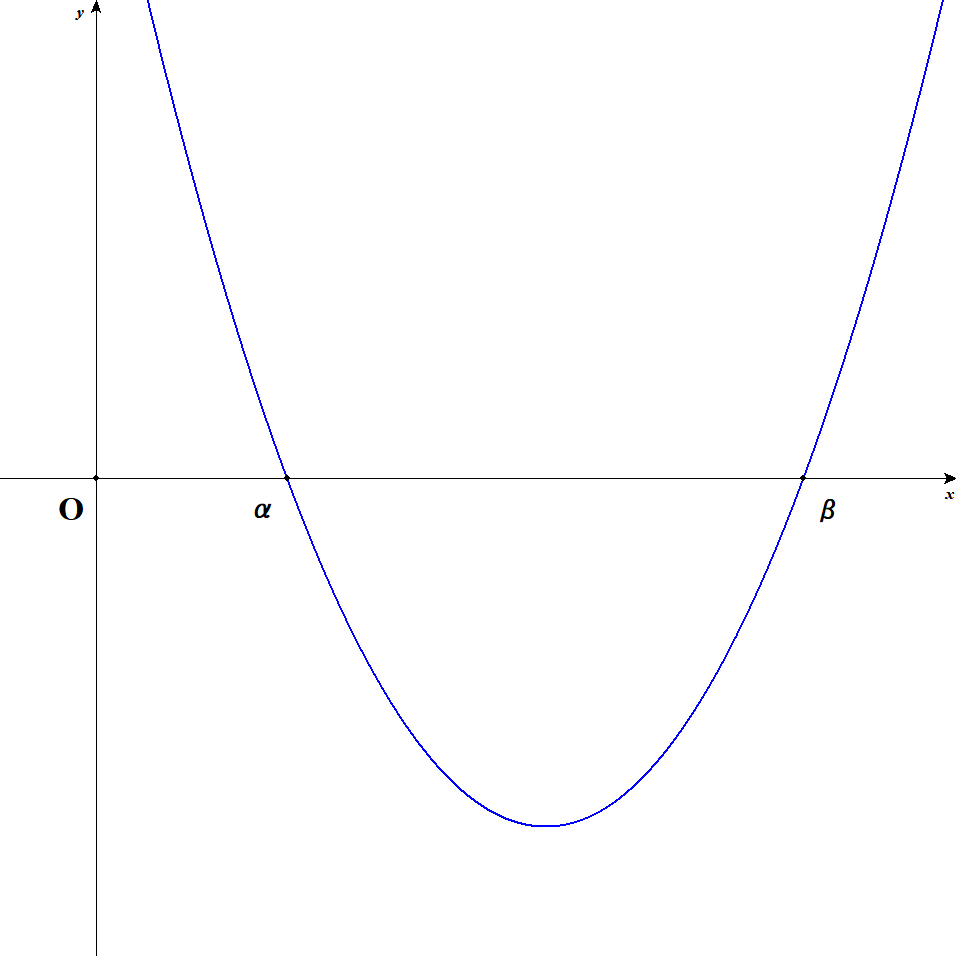
このとき，２次関数の式は次の形で表せます。

\( \begin{align} y = a(x - \alpha)(x - \beta) \end{align} \)

補足なぜこの形か

２次関数の\(x\)切片が\((\alpha, 0), (\beta, 0)\)であるとき，関数の式が\(y = a(x - \alpha)(x - \beta)\)で表せる理由を考えましょう。ただし詳細を理解するには，次回以降で学ぶ２次方程式の知識が必要です。（さらに詳しくは，数学Ⅱで学ぶ因数定理が理解に役立ちます。）

２次関数の式は，一般には\(y = ax^2 + bx + c\)と表せました。 \(x\)切片は，この式で\(y = 0\)となるときの\(x\)の値ですから，次の２次方程式の解です。

\( \begin{align} ax^2 + bx + c = 0 \end{align} \)

\(x\)切片の\(x\)座標が\(\alpha, \beta\)であるということは，この左辺が次の式のように因数分解できるということです。

\( \begin{align} a(x - \alpha)(x - \beta) = 0 \end{align} \)

これで，２次関数の式も次のように因数分解できることが分かります。

\( \begin{align} y &= ax^2 + bx + c \\[5pt] &= a(x - \alpha)(x - \beta) \end{align} \)

次に，\(x\)切片が１つだけの場合も考えましょう。 \(x\)切片の\(x\)座標を\(\alpha\)とします。グラフが次のようになる場合です。

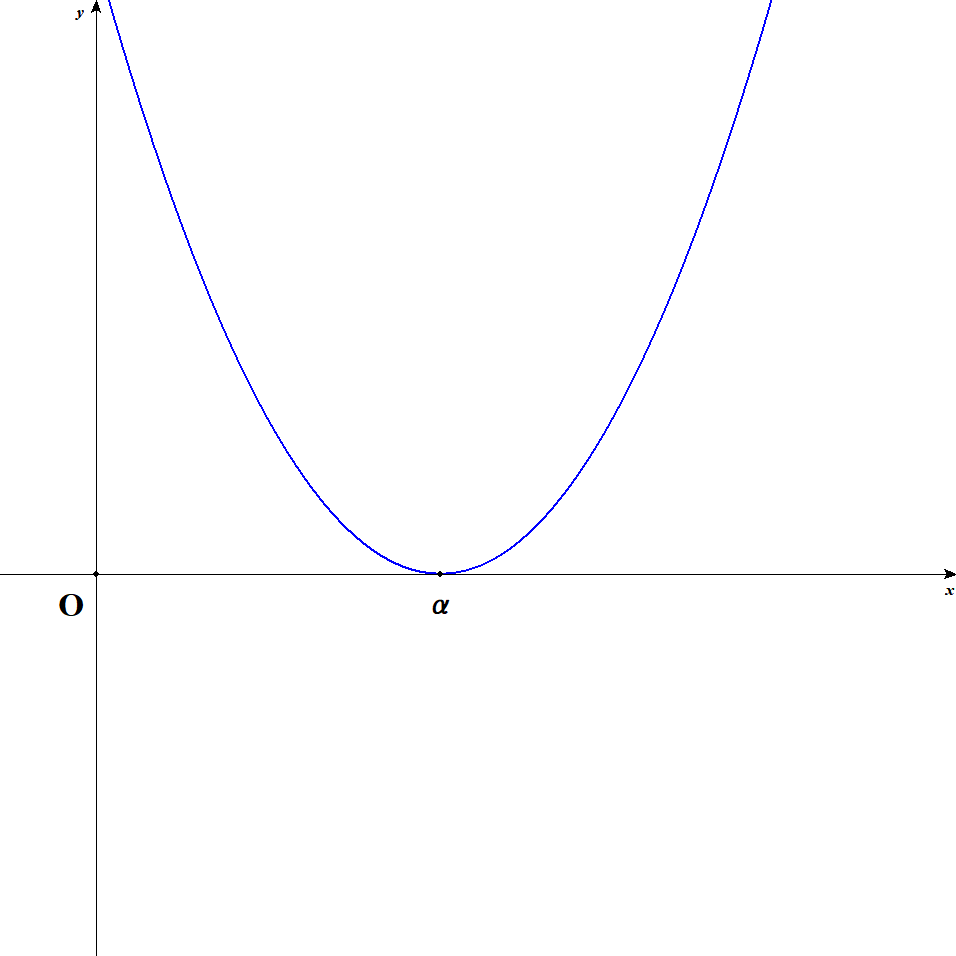
このとき，２次関数の式は次の形で表せます。さきほどの式で\(\beta\)を\(\alpha\)に変えたのと同じ形ですね。

\( \begin{align} y = a(x - \alpha)^2 \end{align} \)

\(x\)切片が１個でも２個でも，\(x\)切片が分かっているときには，未知数は\(a\)ひとつだけですね。

例えば，「グラフの\(x\)切片が\((-1, 0), (1, 0)\)であり，点\((2, 3)\)を通る２次関数を求めよ」という問題を考えてみましょう。 \(x\)切片が分かっているので，２次関数の式は次のように表せます。

\( \begin{align} y = a(x - 1)(x + 1) \end{align} \)

このグラフが点\((2, 3)\)を通るので，その座標を\(x, y\)に代入すれば，\(a\)を求められます。

\( \begin{align} 3 = a(2 - 1)(2 + 1) \end{align} \)

式を整理することで\(a = 1\)と求められ，この２次関数が次の式で表されることが分かりました。

\( \begin{align} y = (x - 1)(x + 1) \end{align} \)

このように，\(x\)切片が分かっているときには，この表し方が便利です。

確認問題

▲

グラフが次の条件を満たす２次関数をそれぞれ求めてください。

３点\((1, 2), (2, 1), (3, -2)\)を通る
\((2, -3)\)を頂点とし，点\((4, 5)\)を通る
\(x\)切片を\((-1, 0), (-3, 0)\)とし，点\((-4, -6)\)を通る

答え

与えられた条件に応じて，計算が楽になるように２次関数の表し方を考えましょう。

３点を通ることだけが分かっていて，頂点や切片は分かりません。この場合は，２次関数を次のように一般形で表すことにしましょう。

\( \begin{align} y = ax^2 + bx + c \end{align} \)

このグラフが３点\((1, 2), (2, 1), (3, -2)\)を通ることから，次の連立方程式が得られます。

\( \begin{eqnarray} \left\{ \begin{array}{l} 2 = a \cdot 1^2 + b \cdot 1 + c\\ 1 = a \cdot 2^2 + b \cdot 2 + c\\ -2 = a \cdot 3^2 + b \cdot 3 + c \end{array} \right. \end{eqnarray} \)

整理すると，次のようになります。

\( \begin{eqnarray} \left\{ \begin{array}{l} a + b + c &= 2 \\ 4a + 2b + c &= 1 \\ 9a + 3b + c &= -2 \end{array} \right. \end{eqnarray} \)

これを解くと，\((a, b, c) = (-1, 2, 1)\)です。したがって，題意の２次関数は\(y = -x^2 + 2x + 1\)です。
頂点が\((2, -3)\)だと分かっているので，題意の２次関数は次のように表せます。

\( \begin{align} y = a(x - 2)^2 - 3 \end{align} \)

このグラフが点\((4, 5)\)を通ることから，次の方程式が得られます。

\( \begin{align} 5 = a(4 - 2)^2 - 3 \end{align} \)

これを整理して解くと，\(a = 2\)です。したがって，題意の２次関数は\(y = 2(x - 2)^2 - 3\)です。
\(x\)切片が\((-1, 0), (-3, 0)\)だと分かっているので，題意の２次関数は次のように表せます。

\( \begin{align} y = a(x + 1)(x + 3) \end{align} \)

このグラフが点\((-4, -6)\)を通ることから，次の方程式が得られます。

\( \begin{align} -6 = a(-4 + 1)(-4 + 3) \end{align} \)

これを整理して解くと，\(a = -2\)です。したがって，題意の２次関数は\(y = -2(x + 1)(x + 3)\)です。

グラフが次の条件を満たす２次関数をそれぞれ求めてください。

\(y = 2x^2\)のグラフを平行移動したもので，２点\((-1, -6), (2, 9)\)を通る
\(y = -3x^2 + 4x + 2\)のグラフを平行移動したもので，２点\((-2, 0), (5, 0)\)を通る

答え

２次関数のグラフの形は，\(x^2\)の係数によって決まります。グラフを平行移動しても，グラフの位置が変わるだけで，形は変わらないことに注意すると，平行移動しても\(x^2\)の係数は変わらないことが分かります。このことを利用すると，計算が簡単に行えます。

頂点や切片の情報が与えられていないので，関数の式は一般形で表すことにしましょう。ただし，グラフの形は平行移動前と変わらないので，\(x^2\)の係数は引き継ぎます。このことを踏まえると，関数は次のように表せます。

\( \begin{align} y = 2x^2 + bx + c \end{align} \)

このグラフが２点\((-1, -6), (2, 9)\)を通ることから，次の連立方程式が得られます。

\( \begin{eqnarray} \left\{ \begin{array}{l} -6 &= 2 \cdot (-1)^2 + b \cdot (-1) + c \\ 9 &= 2 \cdot 2^2 + b \cdot 2 + c \end{array} \right. \end{eqnarray} \)

整理すると，次のようになります。

\( \begin{eqnarray} \left\{ \begin{array}{l} -b + c &= -8 \\ 2b + c &= 1 \end{array} \right. \end{eqnarray} \)

これを解くと，\((b, c) = (3, -5)\)です。したがって，題意の２次関数は\(y = 2x^2 + 3x - 5\)です。
平行移動前のグラフの方程式が分かっているので，\(x^2\)の係数は\(-3\)です。また，\(x\)切片が\((-2, 0), (5, 0)\)ですから，題意の２次関数は次のように表せます。

\( \begin{align} y = -3(x + 2)(x - 5) \end{align} \)